
科目: 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() ,(
,(![]() 为参数,
为参数,![]() 为直线倾斜角).以平面直角坐标系的原点为极点,
为直线倾斜角).以平面直角坐标系的原点为极点,![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程是
的极坐标方程是![]() .
.
(1)当![]() 时,直线
时,直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)已知点![]() 的直角坐标为
的直角坐标为![]() ,直线
,直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,当
两点,当![]() 面积最大时,求直线
面积最大时,求直线![]() 的普通方程.
的普通方程.
查看答案和解析>>
科目: 来源: 题型:
【题目】选修4-4:坐标系与参数方程
以直角坐标系的原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立极坐标系,已知点
轴的正半轴为极轴建立极坐标系,已知点![]() 的直角坐标为
的直角坐标为![]() ,若直线
,若直线![]() 的极坐标方程为
的极坐标方程为![]() 曲线
曲线![]() 的参数方程是
的参数方程是![]() (
(![]() 为参数).
为参数).
(1)求直线![]() 和曲线
和曲线![]() 的普通方程;
的普通方程;
(2)设直线![]() 和曲线
和曲线![]() 交于
交于![]() 两点,求
两点,求![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,以等腰直角三角形ABC的斜边BC上的高AD为折痕,把△ABD和△ACD折成互相垂直的两个平面后,某学生得出下列四个结论:
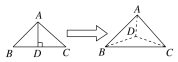
①BD⊥AC;
②△BAC是等边三角形;
③三棱锥D-ABC是正三棱锥;
④平面ADC⊥平面ABC.
其中正确的是( )
A.①②④B.①②③
C.②③④D.①③④
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系中,顶点为原点的抛物线![]() ,它是焦点为椭圆
,它是焦点为椭圆![]() 的右焦点.
的右焦点.
(1)求抛物线![]() 的标准方程;
的标准方程;
(2)过抛物线![]() 的焦点作互相垂直的两条直线分别交抛物线
的焦点作互相垂直的两条直线分别交抛物线![]() 于
于![]() 四点,求四边形
四点,求四边形![]() 的面积的最小值.
的面积的最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】大型综艺节目《最强大脑》中,有一个游戏叫做盲拧魔方,就是玩家先观察魔方状态并进行记忆,记住后蒙住眼睛快速还原魔方,盲拧在外人看来很神奇,其实原理是十分简单的,要学会盲拧也是很容易的.根据调查显示,是否喜欢盲拧魔方与性别有关.为了验证这个结论,某兴趣小组随机抽取了50名魔方爱好者进行调查,得到的情况如下表所示:
喜欢盲拧 | 不喜欢盲拧 | 总计 | |
男 | 23 | 30 | |
女 | 11 | ||
总计 | 50 |
表(1)
并邀请其中20名男生参加盲拧三阶魔方比赛,其完成情况如下表(2)所示.
成功完成时间(分钟) |
|
|
|
|
人数 | 10 | 4 | 4 | 2 |
表(2)
(Ⅰ)将表(1)补充完整,并判断能否在犯错误的概率不超过0.025的前提下认为是否喜欢盲拧与性别有关?
(Ⅱ)现从表(2)中成功完成时间在![]() 和
和![]() 这两组内的6名男生中任意抽取2人对他们的盲拧情况进行视频记录,求2人成功完成时间恰好在同一组内的概率.
这两组内的6名男生中任意抽取2人对他们的盲拧情况进行视频记录,求2人成功完成时间恰好在同一组内的概率.
附参考公式及参考数据:![]() ,其中
,其中![]() .
.
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目: 来源: 题型:
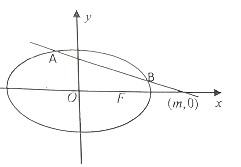
【题目】已知椭圆![]() 的右焦点F与抛物线
的右焦点F与抛物线![]() 焦点重合,且椭圆的离心率为
焦点重合,且椭圆的离心率为![]() ,过
,过![]() 轴正半轴一点
轴正半轴一点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 交椭圆于
交椭圆于![]() 两点.
两点.
(1)求椭圆的标准方程;
(2)是否存在实数![]() 使以线段
使以线段![]() 为直径的圆经过点
为直径的圆经过点![]() ,若存在,求出实数
,若存在,求出实数![]() 的值;若不存在说明理由.
的值;若不存在说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】某企业生产一种产品,根据经验,其次品率Q与日产量x(万件)之间满足关系,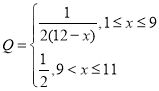 ,已知每生产1万件合格的产品盈利2万元,但每生产1万件次品将亏损1万元(注:次品率=次品数/生产量, 如
,已知每生产1万件合格的产品盈利2万元,但每生产1万件次品将亏损1万元(注:次品率=次品数/生产量, 如![]() 表示每生产10件产品,有1件次品,其余为合格品).
表示每生产10件产品,有1件次品,其余为合格品).
(1)试将生产这种产品每天的盈利额![]() (万元)表示为日产量x(万件)的函数;
(万元)表示为日产量x(万件)的函数;
(2)当日产量为多少时,可获得最大利润?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com