
科目: 来源: 题型:
【题目】已知点的序列![]() ,其中
,其中![]() .(
.(![]() 是线段
是线段![]() 的中点,
的中点,![]() 是线段
是线段![]() 的中点,……,
的中点,……,![]() 是线段
是线段![]() 的中点,…)
的中点,…)
(1)写出![]() 与
与![]() 之间的关系
之间的关系![]() ;
;
(2)设![]() ,计算
,计算![]() ,由此推测数列
,由此推测数列![]() 的通项公式,并且加以证明;
的通项公式,并且加以证明;
(3)求![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,正方形上连接等腰直角三角形,直角三角形上再连接正方形……如此无限重复下去,设正方形面积为![]() ,三角形面积为
,三角形面积为![]() .当第一个正方形的边长为2时,则这些正方形和三角形的面积的总和为______.
.当第一个正方形的边长为2时,则这些正方形和三角形的面积的总和为______.
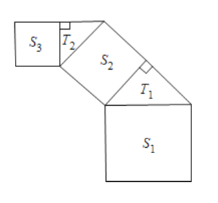
查看答案和解析>>
科目: 来源: 题型:
【题目】某班教室桌椅6排7列,有40名同学.空出最后一排的某两个位置,其余人按身高和视力排座位.班中有24人身高高,有18人视力好,其中,有6名同学同时具备此两个条件.已知若一名同学个子矮视力又不好,则他必须坐在前三排;若一名同学个子高视力又好,则他必须坐在最后三排.设排座位的方法是![]() ,则
,则![]() 的质因数分解中的2的次数是______.
的质因数分解中的2的次数是______.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知两个不同的单位向量![]() 与
与![]() 之间满足关系:
之间满足关系:![]() ,其中
,其中![]() .
.
(1)若![]() ,求
,求![]() 的解析式;
的解析式;
(2)![]() 能否和
能否和![]() 垂直?
垂直?![]() 能否和
能否和![]() 平行?若不能,则说明理由;若能,则求出对应的k值;
平行?若不能,则说明理由;若能,则求出对应的k值;
(3)求![]() 与
与![]() 夹角的最大值.
夹角的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).
为参数).![]() 是曲线
是曲线![]() 上的动点,将线段
上的动点,将线段![]() 绕
绕![]() 点顺时针旋转
点顺时针旋转![]() 得到线段
得到线段![]() ,设点
,设点![]() 的轨迹为曲线
的轨迹为曲线![]() .以坐标原点
.以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系.
轴正半轴为极轴建立极坐标系.
(I)求曲线![]() ,
,![]() 的极坐标方程;
的极坐标方程;
(II)在(I)的条件下,若射线![]() 与曲线
与曲线![]() ,
,![]() 分别交于
分别交于![]() 两点(除极点外),且有定点
两点(除极点外),且有定点![]() ,求
,求![]() 面积.
面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知无穷等比数列![]() 的首项、公比均为
的首项、公比均为![]() .
.
(1)试求无穷等比子数列![]() 各项的和;
各项的和;
(2)是否存在数列![]() 的一个无穷等比子数列,使得它各项的和为
的一个无穷等比子数列,使得它各项的和为![]() ?若存在,求出所有满足条件的子数列的通项公式;若不存在,请说明理由.
?若存在,求出所有满足条件的子数列的通项公式;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知数列![]() 满足
满足![]() ,且
,且![]() ,点
,点![]() 在二次函数
在二次函数![]() 的图象上.
的图象上.
(1)试判断数列![]() 是否为算术平方根递推数列?若是,请说明你的理由;
是否为算术平方根递推数列?若是,请说明你的理由;
(2)记![]() ,求证:数列
,求证:数列![]() 是等比数列,并求出通项公式
是等比数列,并求出通项公式![]() ;
;
(3)在数列![]() 中依据某种顺序从左至右取出其中的项
中依据某种顺序从左至右取出其中的项![]() ,…,把这些项重新组成一个新数列
,…,把这些项重新组成一个新数列![]() ,….若数列
,….若数列![]() 是首项为
是首项为![]() 、公比为
、公比为![]() 的无穷等比数列,且数列
的无穷等比数列,且数列![]() 各项的和为
各项的和为![]() ,求正整数
,求正整数![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com