
科目: 来源: 题型:
【题目】已知抛物线![]() 的焦点为F,直线l过点
的焦点为F,直线l过点![]() .
.
(1)若点F到直线l的距离为![]() ,求直线l的斜率;
,求直线l的斜率;
(2)设A,B为抛物线上两点,且AB不与x轴垂直,若线段AB的垂直平分线恰过点M,求证:线段AB中点的横坐标为定值
查看答案和解析>>
科目: 来源: 题型:
【题目】从一批草莓中,随机抽取50个,其重量(单位:克)的频数分布表如下:
分组(重量) |
|
|
|
|
须数(个) | 10 | 5 | 20 | 15 |
(1)根据频数分布表计算草莓的重量在![]() 的频率;
的频率;
(2)用分层抽样的方法从重量在![]() 和
和![]() 的草莓中共抽取5个,其中重量在
的草莓中共抽取5个,其中重量在![]() 的有几个?
的有几个?
(3)从(2)中抽出的5个草莓中任取2个,求重量在![]() 和
和![]() 中各有1个的概率.
中各有1个的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】现有10件产品中有3件次品,7件正品,从中抽取5件![]() 用数字表示
用数字表示![]()
(1)没有次品的抽法有多少种?
(2)有2件次品的抽法有多少种?
(3)至少1件次品的抽法有多少种?
查看答案和解析>>
科目: 来源: 题型:
【题目】现有10名教师,其中男教师6名,女教师4名.
(1)现要从中选2名去参加会议,有多少种不同的选法?
(2)选出2名男教师或2名女教师去外地学习的选法有多少种?
(3)现要从中选出男、女老师各2名去参加会议,有多少种不同的选法?
查看答案和解析>>
科目: 来源: 题型:
【题目】田忌赛马是![]() 史记
史记![]() 中记载的一个故事,说的是齐国将军田忌经常与齐国众公子赛马,孙膑发也们的马脚力都差不多,都分为上、中、下三等
中记载的一个故事,说的是齐国将军田忌经常与齐国众公子赛马,孙膑发也们的马脚力都差不多,都分为上、中、下三等![]() 于是孙膑给田忌将军制定了一个必胜策略:比赛即将开始时,他让田忌用下等马对战公子们的上等马,用上等马对战公子们的中等马,用中等马对战公子们的下等马,从而使田忌赢得公子们许多赌注
于是孙膑给田忌将军制定了一个必胜策略:比赛即将开始时,他让田忌用下等马对战公子们的上等马,用上等马对战公子们的中等马,用中等马对战公子们的下等马,从而使田忌赢得公子们许多赌注![]() 假设田忌的各等级马与某公子的各等级马进行一场比赛获胜的概率如表所示:
假设田忌的各等级马与某公子的各等级马进行一场比赛获胜的概率如表所示:
田忌的马 | 上等马 | 中等马 | 下等马 |
上等马 |
|
| 1 |
中等马 |
|
|
|
下等马 | 0 |
|
|
比赛规则规定:一次比由三场赛马组成,每场由公子和田忌各出一匹马出骞,结果只有胜和负两种,并且毎一方三场赛马的马的等级各不相同,三场比赛中至少获胜两场的一方为最终胜利者.
![]() 如果按孙膑的策略比赛一次,求田忌获胜的概率;
如果按孙膑的策略比赛一次,求田忌获胜的概率;
![]() 如果比赛约定,只能同等级马对战,每次比赛赌注1000金,即胜利者赢得对方1000金,每月比赛一次,求田忌一年赛马获利的数学期望.
如果比赛约定,只能同等级马对战,每次比赛赌注1000金,即胜利者赢得对方1000金,每月比赛一次,求田忌一年赛马获利的数学期望.
查看答案和解析>>
科目: 来源: 题型:
【题目】关于![]() 的说法,正确的是( )
的说法,正确的是( )
A.展开式中的二项式系数之和为1024B.展开式中第6项的二项式系数最大
C.展开式中第5项和第7项的二项式系数最大D.展开式中第6项的系数最小
查看答案和解析>>
科目: 来源: 题型:
【题目】1642年,帕斯卡发明了一种可以进行十进制加减法的机械计算机![]() 年,莱布尼茨改进了帕斯卡的计算机,但莱布尼兹认为十进制的运算在计算机上实现起来过于复杂,随即提出了“二进制”数的概念
年,莱布尼茨改进了帕斯卡的计算机,但莱布尼兹认为十进制的运算在计算机上实现起来过于复杂,随即提出了“二进制”数的概念![]() 之后,人们对进位制的效率问题进行了深入的研究
之后,人们对进位制的效率问题进行了深入的研究![]() 研究方法如下:对于正整数
研究方法如下:对于正整数![]() ,
,![]() ,我们准备
,我们准备![]() 张不同的卡片,其中写有数字0,1,…,
张不同的卡片,其中写有数字0,1,…,![]() 的卡片各有
的卡片各有![]() 张
张![]() 如果用这些卡片表示
如果用这些卡片表示![]() 位
位![]() 进制数,通过不同的卡片组合,这些卡片可以表示
进制数,通过不同的卡片组合,这些卡片可以表示![]() 个不同的整数
个不同的整数![]() 例如
例如![]() ,
,![]() 时,我们可以表示出
时,我们可以表示出![]() 共
共![]() 个不同的整数
个不同的整数![]() 假设卡片的总数
假设卡片的总数![]() 为一个定值,那么
为一个定值,那么![]() 进制的效率最高则意味着
进制的效率最高则意味着![]() 张卡片所表示的不同整数的个数
张卡片所表示的不同整数的个数![]() 最大
最大![]() 根据上述研究方法,几进制的效率最高?
根据上述研究方法,几进制的效率最高?![]()
![]()
A. 二进制 B. 三进制 C. 十进制 D. 十六进制
查看答案和解析>>
科目: 来源: 题型:
【题目】椭圆![]() (
(![]() )的离心率是
)的离心率是![]() ,点
,点![]() 在短轴
在短轴![]() 上,且
上,且![]() 。
。
(1)球椭圆![]() 的方程;
的方程;
(2)设![]() 为坐标原点,过点
为坐标原点,过点![]() 的动直线与椭圆交于
的动直线与椭圆交于![]() 两点。是否存在常数
两点。是否存在常数![]() ,使得
,使得![]() 为定值?若存在,求
为定值?若存在,求![]() 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
查看答案和解析>>
科目: 来源: 题型:
【题目】某社区消费者协会为了解本社区居民网购消费情况,随机抽取了100位居民作为样本,就最近一年来网购消费金额(单位:千元),网购次数和支付方式等进行了问卷调査.经统计这100位居民的网购消费金额均在区间![]() 内,按
内,按![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分成6组,其频率分布直方图如图所示.
分成6组,其频率分布直方图如图所示.
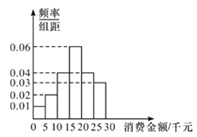
(1)估计该社区居民最近一年来网购消费金额的中位数;
(2)将网购消费金额在20千元以上者称为“网购迷”,补全下面的![]() 列联表,并判断有多大把握认为“网购迷与性别有关系”;
列联表,并判断有多大把握认为“网购迷与性别有关系”;
男 | 女 | 合计 | |
网购迷 | 20 | ||
非网购迷 | 45 | ||
合计 | 100 |
(3)调査显示,甲、乙两人每次网购采用的支付方式相互独立,两人网购时间与次数也互不. 影响.统计最近一年来两人网购的总次数与支付方式,所得数据如下表所示:
网购总次数 | 支付宝支付次数 | 银行卡支付次数 | 微信支付次数 | |
甲 | 80 | 40 | 16 | 24 |
乙 | 90 | 60 | 18 | 12 |
将频率视为概率,若甲、乙两人在下周内各自网购2次,记两人采用支付宝支付的次数之和为![]() ,求
,求![]() 的数学期望.
的数学期望.
附:观测值公式: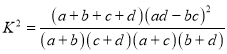
临界值表:
| 0.01 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com