
【题目】1642年,帕斯卡发明了一种可以进行十进制加减法的机械计算机![]() 年,莱布尼茨改进了帕斯卡的计算机,但莱布尼兹认为十进制的运算在计算机上实现起来过于复杂,随即提出了“二进制”数的概念
年,莱布尼茨改进了帕斯卡的计算机,但莱布尼兹认为十进制的运算在计算机上实现起来过于复杂,随即提出了“二进制”数的概念![]() 之后,人们对进位制的效率问题进行了深入的研究
之后,人们对进位制的效率问题进行了深入的研究![]() 研究方法如下:对于正整数
研究方法如下:对于正整数![]() ,
,![]() ,我们准备
,我们准备![]() 张不同的卡片,其中写有数字0,1,…,
张不同的卡片,其中写有数字0,1,…,![]() 的卡片各有
的卡片各有![]() 张
张![]() 如果用这些卡片表示
如果用这些卡片表示![]() 位
位![]() 进制数,通过不同的卡片组合,这些卡片可以表示
进制数,通过不同的卡片组合,这些卡片可以表示![]() 个不同的整数
个不同的整数![]() 例如
例如![]() ,
,![]() 时,我们可以表示出
时,我们可以表示出![]() 共
共![]() 个不同的整数
个不同的整数![]() 假设卡片的总数
假设卡片的总数![]() 为一个定值,那么
为一个定值,那么![]() 进制的效率最高则意味着
进制的效率最高则意味着![]() 张卡片所表示的不同整数的个数
张卡片所表示的不同整数的个数![]() 最大
最大![]() 根据上述研究方法,几进制的效率最高?
根据上述研究方法,几进制的效率最高?![]()
![]()
A. 二进制 B. 三进制 C. 十进制 D. 十六进制
科目:高中数学 来源: 题型:
【题目】以平面直角坐标系的原点为极点,![]() 轴的正半轴为极轴,建立极坐标系,已知直线
轴的正半轴为极轴,建立极坐标系,已知直线![]() 的参数方程是
的参数方程是 (m>0,t为参数),曲线
(m>0,t为参数),曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与曲线
,与曲线![]() 交于点
交于点![]() ,且
,且![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现将甲、乙两个学生在高二的6次数学测试的成绩(百分制)制成如图所示的茎叶图,进入高三后,由于改进了学习方法,甲、乙这两个学生的考试成绩预计同时有了大的提升:若甲(乙)的高二任意一次考试成绩为![]() ,则甲(乙)的高三对应的考试成绩预计为
,则甲(乙)的高三对应的考试成绩预计为![]() .
.

(1)试预测:高三6次测试后,甲、乙两个学生的平均成绩分别为多少?谁的成绩更稳定?
(2)若已知甲、乙两个学生的高二6次考试成绩分别由低到高进步的,定义![]() 为高三的任意一次考试后甲、乙两个学生的当次成绩之差的绝对值,求
为高三的任意一次考试后甲、乙两个学生的当次成绩之差的绝对值,求![]() 的平均值.
的平均值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年是中国传统的农历“鼠年”,有人用3个圆构成“卡通鼠”的形象,如图:![]() 是圆Q的圆心,圆Q过坐标原点O;点L、S均在x轴上,圆L与圆S的半径都等于2,圆S、圆L均与圆Q外切.已知直线l过点O.
是圆Q的圆心,圆Q过坐标原点O;点L、S均在x轴上,圆L与圆S的半径都等于2,圆S、圆L均与圆Q外切.已知直线l过点O.

(1)若直线l与圆L、圆S均相切,则l截圆Q所得弦长为__________;
(2)若直线l截圆L、圆S、圆Q所得弦长均等于d,则![]() __________.
__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P-ABC中,D,E,F分别为棱PC,AC,AB的中点,PA⊥平面ABC,∠ABC=90°,AB=PA=6,BC=8,则( )
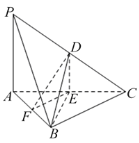
A.三棱锥D-BEF的体积为6
B.直线PB与直线DF垂直
C.平面DEF截三棱锥P-ABC所得的截面面积为12
D.点P与点A到平面BDE的距离相等
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从一批草莓中,随机抽取50个,其重量(单位:克)的频数分布表如下:
分组(重量) |
|
|
|
|
须数(个) | 10 | 5 | 20 | 15 |
(1)根据频数分布表计算草莓的重量在![]() 的频率;
的频率;
(2)用分层抽样的方法从重量在![]() 和
和![]() 的草莓中共抽取5个,其中重量在
的草莓中共抽取5个,其中重量在![]() 的有几个?
的有几个?
(3)从(2)中抽出的5个草莓中任取2个,求重量在![]() 和
和![]() 中各有1个的概率.
中各有1个的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,将椭圆![]() 上每一点的横坐标保持不变,纵坐标变为原来的一半,得曲线C,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,直线l的极坐标方程为
上每一点的横坐标保持不变,纵坐标变为原来的一半,得曲线C,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,直线l的极坐标方程为![]() .
.
![]() 写出曲线C的普通方程和直线l的直角坐标方程;
写出曲线C的普通方程和直线l的直角坐标方程;
![]() 已知点
已知点![]() 且直线l与曲线C交于A、B两点,求
且直线l与曲线C交于A、B两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某超市在节日期间进行有奖促销,凡在该超市购物满400元的顾客,将获得一次摸奖机会,规则如下:奖盒中放有除颜色外完全相同的1个红球,1个黄球,1个白球和1个黑球顾客不放回的每次摸出1个球,若摸到黑球则停止摸奖,否则就继续摸球规定摸到红球奖励20元,摸到白球或黄球奖励10元,摸到黑球不奖励
(1)求1名顾客摸球2次停止摸奖的概率:
(2)记![]() 为1名顾客5次摸奖获得的奖金数额,求随机变量
为1名顾客5次摸奖获得的奖金数额,求随机变量![]() 的分布列和数学期望
的分布列和数学期望
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com