
科目: 来源: 题型:
【题目】已知椭圆![]() 的焦距与短轴长相等,长轴长为
的焦距与短轴长相等,长轴长为![]() ,设过右焦点F倾斜角为
,设过右焦点F倾斜角为![]() 的直线交椭圆M于A、B两点.
的直线交椭圆M于A、B两点.
(1)求椭圆M的方程;
(2)求证:![]()
(3)设过右焦点F且与直线AB垂直的直线交椭圆M于C、D,求四边形ABCD面积的最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】2020年寒假,因为“新冠”疫情全体学生只能在家进行网上学习,为了研究学生网上学习的情况,某学校随机抽取![]() 名学生对线上教学进行调查,其中男生与女生的人数之比为
名学生对线上教学进行调查,其中男生与女生的人数之比为![]() ,抽取的学生中男生有
,抽取的学生中男生有![]() 人对线上教学满意,女生中有
人对线上教学满意,女生中有![]() 名表示对线上教学不满意.
名表示对线上教学不满意.
(1)完成![]() 列联表,并回答能否有
列联表,并回答能否有![]() 的把握认为“对线上教学是否满意 与性别有关”;
的把握认为“对线上教学是否满意 与性别有关”;
态度 性别 | 满意 | 不满意 | 合计 |
男生 | |||
女生 | |||
合计 | 100 |
(2)从被调查的对线上教学满意的学生中,利用分层抽样抽取![]() 名学生,再在这
名学生,再在这![]() 名学生中抽取
名学生中抽取![]() 名学生,作线上学习的经验介绍,求其中抽取一名男生与一名女生的概率.
名学生,作线上学习的经验介绍,求其中抽取一名男生与一名女生的概率.
附: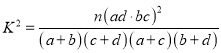 .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目: 来源: 题型:
【题目】某国有53座城市,任意两座城市之间要么有一条双向公路直达,要么没有直接相连的公路。已知这53座城市之间共有312条公路,并且由任何一座城市出发通过公路均能到达其余各城市。每一座城市至多向其余12座城市引出公路,且每走一条公路需要缴纳10元路费。现甲在城市A,且身上仅有120元。甲是否一定能到达任意一座城市?证明你的结论。
查看答案和解析>>
科目: 来源: 题型:
【题目】设![]() 表示k个数字均为1的十进制数(如
表示k个数字均为1的十进制数(如![]() =1,
=1,![]() =111),定义
=111),定义![]() 。
。
(1)对于任意正整数m、n,令![]() ,写出一个关于f(m,n)的递推关系式,并证明之;
,写出一个关于f(m,n)的递推关系式,并证明之;
(2)证明:对于任意正整数m、n,{m+n}!均可以被{m}!.{n}!整除。
查看答案和解析>>
科目: 来源: 题型:
【题目】将具有如下性质的3×3方格表称为“T-网格”:
(1)五个格填1,四个格填0;
(2)三行、三列以及两条对角线共八条线上至多有一条,其中三个数两两相等。
则不同的T-网格共有________个。
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系中,曲线C的参数方程为![]() (
(![]() 为参数),以平面直角坐标系的原点O为极点,x轴正半轴为极轴建立极坐标系.
为参数),以平面直角坐标系的原点O为极点,x轴正半轴为极轴建立极坐标系.
(1)求曲线C的极坐标方程;
(2)过点![]() ,倾斜角为
,倾斜角为![]() 的直线l与曲线C相交于M,N两点,求
的直线l与曲线C相交于M,N两点,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,以椭圆E的长轴和短轴为对角线的四边形的面积为
,以椭圆E的长轴和短轴为对角线的四边形的面积为![]() .
.
(1)求椭圆E的方程;
(2)若直线![]() 与椭圆E相交于A,B两点,设P为椭圆E上一动点,且满足
与椭圆E相交于A,B两点,设P为椭圆E上一动点,且满足![]() (O为坐标原点).当
(O为坐标原点).当![]() 时,求
时,求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com