【题目】已知数列前项和为，且.

（1）证明数列是等比数列；

（2）设，求数列的前项和.

【题目】已知定义在上的函数满足且，若恒成立，则实数的取值范围为______．

【题目】我国南北朝时期的数学家张丘建是世界数学史上解决不定方程的第一人，他在《张丘建算经》中给出一个解不定方程的百鸡问题，问题如下：鸡翁一，值钱五，鸡母一，值钱三，鸡雏三，值钱一．百钱买百鸡，问鸡翁母雏各几何？用代数方法表述为：设鸡翁、鸡母、鸡雏的数量分别为，，，则鸡翁、鸡母、鸡雏的数量即为方程组的解．其解题过程可用框图表示如下图所示，则框图中正整数的值为 ______．

【题目】已知点是双曲线的左右焦点，其渐近线为，且其右焦点与抛物线的焦点重合.

（1）求双曲线的方程；

（2）过的直线与相交于两点，直线的法向量为，且，求的值

（3）在（2）的条件下，若双曲线在第四象限的部分存在一点满足，求的值及的面积.

【题目】如图，底面为矩形的四棱锥，底面，，，是的中点.

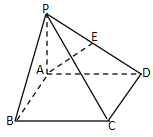
（1）求四棱锥的体积；

（2）求与面所成角；

（3）在边上是否存在一点，使得到平面的距离为？若存在，求出；若不存在，请说明理由.

【题目】已知椭圆的右焦点为,坐标原点为.椭圆的动弦过右焦点且不垂直于坐标轴， 的中点为,过且垂直于线段的直线交射线于点

(I)证明:点在直线上;

(Ⅱ)当四边形是平行四边形时,求的面积.

①直线上有两个点到平面的距离相等，则这条直线和这个平面平行；

②过球面上任意两点的大圆有且只有一个；

③直四棱柱是直平行六面体；

④为异面直线，则过且与平行的平面有且仅有一个；

⑤两相邻侧面所成角相等的棱锥是正棱锥.

【题目】已知函数，

（Ⅰ）若，且是函数的一个极值，求函数的最小值；

（Ⅱ）若，求证：，.

记x表示1台机器在三年使用期内的维修次数，y表示1台机器在维修上所需的费用（单位：元），表示购机的同时购买的维修服务次数.

（1）若=10，求y与x的函数解析式；

（2）若要求“维修次数不大于”的频率不小于0.8，求n的最小值；

（3）假设这100台机器在购机的同时每台都购买10次维修服务，或每台都购买11次维修服务，分别计算这100台机器在维修上所需费用的平均数，以此作为决策依据，购买1台机器的同时应购买10次还是11次维修服务？

【题目】分形几何学是一门以不规则几何形态为研究对象的几何学．分形的外表结构极为复杂，但其内部却是有规律可寻的．一个数学意义上分形的生成是基于一个不断迭代的方程式，即一种基于递归的反馈系统．下面我们用分形的方法来得到一系列图形，如图1，线段的长度为a，在线段上取两个点，，使得，以为一边在线段的上方做一个正六边形，然后去掉线段，得到图2中的图形；对图2中的最上方的线段作相同的操作，得到图3中的图形；依此类推，我们就得到了以下一系列图形：

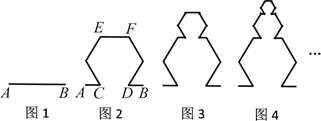
记第个图形（图1为第1个图形）中的所有线段长的和为，现给出有关数列的四个命题：

①数列是等比数列；

②数列是递增数列；

③存在最小的正数，使得对任意的正整数 ，都有 ；

④存在最大的正数，使得对任意的正整数，都有．

其中真命题的序号是________________（请写出所有真命题的序号）.