【题目】已知抛物线：.

（1）若直线经过抛物线的焦点，求抛物线的准线方程；

（2）若斜率为-1的直线经过抛物线的焦点，且与抛物线交于，两点，当时，求抛物线的方程.

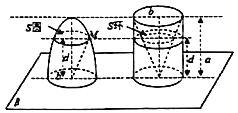
【题目】我国齐梁时代的数学家祖暅提出了一条原理：“幂势既同，则积不容异”.意思是：两个等高的几何体若在所有等高处的水平截面的面积相等，则这两个几何体的体积相等.椭球体是椭圆绕其轴旋转所成的旋转体.如图，将底面直径都为，高皆为的椭半球体和已被挖去了圆锥体的圆柱放置于同一平面上，用平行于平面且与平面任意距离处的平面截这两个几何体，可横截得到及两截面.可以证明总成立.据此，半短轴长为1，半长轴长为3的椭球体的体积是_______．

A. B. π C. 2 D.

A.一条直线与两个平行平面中的一个相交，则必与另一个平面相交.

B.平行于同一平面的两条直线一定平行.

C.如果平面不垂直于平面，那么平面内一定不存在直线垂直于平面.

D.若直线不平行于平面，且不在平面内，则在平面内不存在与平行的直线.

【题目】已知椭圆：，该椭圆经过点，且离心率为.

（1）求椭圆的标准方程；

（2）设是圆上任意一点，由引椭圆的两条切线，，当两条切线的斜率都存在时，证明：两条切线斜率的积为定值.

【题目】已知抛物线：.

（1）若直线经过抛物线的焦点，求抛物线的准线方程；

（2）若斜率为-1的直线经过抛物线的焦点，且与抛物线交于，两点，当时，求抛物线的方程.

并对不同年龄层的市民对这款电视机的购买意愿作出调查，得到的数据如下表所示：

（1）根据图中的数据，试估计该款电视机的平均使用时间；

（2）根据表中数据，判断是否有99.9%的把握认为“愿意购买该款电视机”与“市民的年龄”有关；

（3）若按照电视机的使用时间进行分层抽样，从使用时间在和的电视机中抽取5台，再从这5台中随机抽取2台进行配件检测，求被抽取的2台电视机的使用时间都在内的概率．

A.一条直线与两个平行平面中的一个相交，则必与另一个平面相交.

B.平行于同一平面的两条直线一定平行.

C.如果平面不垂直于平面，那么平面内一定不存在直线垂直于平面.

D.若直线不平行于平面，且不在平面内，则在平面内不存在与平行的直线.

【题目】已知函数

（1）若，求函数的单调区间；

（2）若关于的不等式在上恒成立，求实数的取值范围．

【题目】已知椭圆：的右焦点为，上顶点为，直线的斜率为，且原点到直线的距离为.

（1）求椭圆的标准方程；

（2）若不经过点的直线：与椭圆交于两点，且与圆相切.试探究的周长是否为定值，若是，求出定值；若不是，请说明理由.