【题目】在直角坐标系中，曲线C的参数方程为 (其中为参数)，以坐标原点为极点，轴的正半轴为极轴建立极坐标系中，直线的极坐标方程为.

（Ⅰ）求C的普通方程和直线的倾斜角；

（Ⅱ）设点(0，2)，和交于两点，求.

【题目】已知平面上的线段及点，任取上一点，线段长度的最小值称为点到线段的距离，记作.请你写出到两条线段，距离相等的点的集合，，，其中，，，，，是下列两组点中的一组．对于下列两种情形，只需选做一种，满分分别是① 3分；② 5分．① ，，，；② ，，，．你选择第_____种情形，到两条线段，距离相等的点的集合_____________.

【题目】甲、乙两位同学分别做下面这道题目：在平面直角坐标系中，动点到的距离比到轴的距离大，求的轨迹.甲同学的解法是：解：设的坐标是，则根据题意可知

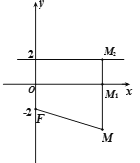
，化简得； ①当时，方程可变为；②这表示的是端点在原点、方向为轴正方向的射线，且不包括原点； ③当时，方程可变为； ④这表示以为焦点，以直线为准线的抛物线；⑤所以的轨迹为端点在原点、方向为轴正方向的射线，且不包括原点和以为焦点，以直线为准线的抛物线. 乙同学的解法是：解：因为动点到的距离比到轴的距离大. ①如图，过点作轴的垂线，垂足为. 则.设直线与直线的交点为，则； ②即动点到直线的距离比到轴的距离大； ③所以动点到的距离与到直线的距离相等；④所以动点的轨迹是以为焦点，以直线为准线的抛物线； ⑤甲、乙两位同学中解答错误的是________（填“甲”或者“乙”），他的解答过程是从_____处开始出错的（请在横线上填写① 、②、③、④ 或⑤ ）.

【题目】已知（为常数）.

（1）求的极值；

（2）设，记，已知为函数是两个零点，求证： .

【题目】已知函数()，曲线在点处的切线方程为.

(1)求实数的值，并求的单调区间；

(2)试比较与的大小，并说明理由；

(3)求证：

【题目】如图所示，在平行四边形中，点是边的中点，将沿折起，使点到达点的位置，且

（1）求证; 平面平面；

（2）若平面和平面的交线为，求二面角的余弦值.

①命题“若x2－3x＋2＝0，则x＝1”的逆否命题为：若x≠1，则x2－3x＋2≠0

②x＝1是x2－3x＋2＝0的充分不必要条件

③若p∧q为假命题，则p，q均为假命题

④对于命题p：x∈R，使得x2＋x＋1<0，则非p：x∈R， 均有x2＋x＋1≥0

【题目】已知椭圆的左右焦点分别为F1，F2，离心率为，设过点F2的直线l被椭圆C截得的线段为MN，当l⊥x轴时，|MN|＝3．

（1）求椭圆C的标准方程；

（2）在x轴上是否存在一点P，使得当l变化时，总有PM与PN所在的直线关于x轴对称？若存在，请求出点P的坐标；若不存在，请说明理由．

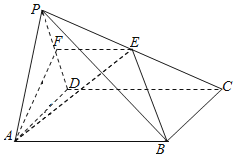
（1）求证：AB∥EF；

（2）若PA＝PD＝AD，且平面PAD⊥平面ABCD，求平面PAF与平面AFE所成的锐二面角的余弦值．

【题目】已知点F是拋物线C:y2=2px(p>0)的焦点,点M(x0,1)在C上,且|MF|=.

(1)求p的值;

(2)若直线l经过点Q(3,-1)且与C交于A,B(异于M)两点,证明:直线AM与直线BM的斜率之积为常数.