
科目: 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系,曲线
轴的非负半轴为极轴建立极坐标系,曲线![]() 的极坐标方程是
的极坐标方程是![]()
(Ⅰ)求直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,当
两点,当![]() 时,求
时,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示的几何体,是将高为2、底面半径为1的圆柱沿过旋转轴的平面切开后,将其中一半沿切面向右水平平移后形成的封闭体.![]() 分别为
分别为![]() 的中点,
的中点,![]() 为弧
为弧![]() 的中点,
的中点,![]() 为弧
为弧![]() 的中点.
的中点.
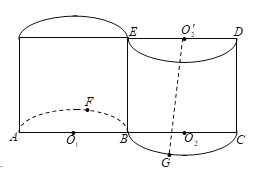
(1)求直线![]() 与底面
与底面![]() 所成的角的大小;
所成的角的大小;
(2)求异面直线![]() 与
与![]() 所成的角的大小(结果用反三角函数值表示).
所成的角的大小(结果用反三角函数值表示).
查看答案和解析>>
科目: 来源: 题型:
【题目】现将甲、乙、丙、丁四个人安排到座位号分别是![]() 的四个座位上,他们分别有以下要求,
的四个座位上,他们分别有以下要求,
甲:我不坐座位号为![]() 和
和![]() 的座位;
的座位;
乙:我不坐座位号为![]() 和
和![]() 的座位;
的座位;
丙:我的要求和乙一样;
丁:如果乙不坐座位号为![]() 的座位,我就不坐座位号为
的座位,我就不坐座位号为![]() 的座位.
的座位.
那么坐在座位号为![]() 的座位上的是( )
的座位上的是( )
A. 甲B. 乙C. 丙D. 丁
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知椭圆![]() ,左、右焦点分别为
,左、右焦点分别为![]() ,
,![]() ,右顶点为
,右顶点为![]() ,上顶点为
,上顶点为![]() ,
,![]() 为椭圆上在第一象限内一点.
为椭圆上在第一象限内一点.
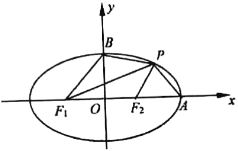
(1)若![]() .
.
①求椭圆的离心率![]() ;
;
②求直线![]() 的斜率.
的斜率.
(2)若![]() ,
,![]() ,
,![]() 成等差数列,且
成等差数列,且![]() ,求直线
,求直线![]() 的斜率的取值范围.
的斜率的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知正方形![]() 和矩形
和矩形![]() 所在的平面互相垂直,
所在的平面互相垂直,![]() ,
,![]() ,
,![]() 是线段
是线段![]() 的中点.
的中点.
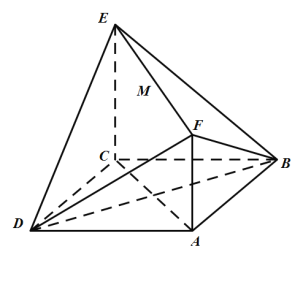
(1)求证:![]() 平面
平面![]() ;
;
(2)若![]() ,求二面角
,求二面角![]() 的大小;
的大小;
(3)若线段![]() 上总存在一点
上总存在一点![]() ,使得
,使得![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】2018年“双十一”全网销售额达![]() 亿元,相当于全国人均消费
亿元,相当于全国人均消费![]() 元,同比增长
元,同比增长![]() ,监测参与“双十一”狂欢大促销的
,监测参与“双十一”狂欢大促销的![]() 家电商平台有天猫、京东、苏宁易购、网易考拉在内的综合性平台,有拼多多等社交电商平台,有敦煌网、速卖通等出口电商平台.某大学学生社团在本校
家电商平台有天猫、京东、苏宁易购、网易考拉在内的综合性平台,有拼多多等社交电商平台,有敦煌网、速卖通等出口电商平台.某大学学生社团在本校![]() 名大一学生中采用男女分层抽样,分别随机调查了若干个男生和
名大一学生中采用男女分层抽样,分别随机调查了若干个男生和![]() 个女生的网购消费情况,制作出男生的频率分布表、直方图(部分)和女生的茎叶图如下:
个女生的网购消费情况,制作出男生的频率分布表、直方图(部分)和女生的茎叶图如下:

男生直方图
分组(百元) | 男生人数 | 频率 |
|
|
|
|
|
|
|
|
|
|
| |
|
| |
|
|
|
|
|
|
|
|
|
合计 |
|

女生茎叶图
(1)请完成频率分布表的三个空格,并估计该校男生网购金额的中位数(单位:元,精确到个位).
(2)若网购为全国人均消费的三倍以上称为“剁手党”,估计该校大一学生中的“剁手党”人数为多少?从抽样数据中网购不足![]() 元的同学中随机抽取
元的同学中随机抽取![]() 人发放纪念品,则
人发放纪念品,则![]() 人都是女生的概率为多少?
人都是女生的概率为多少?
(3)用频率估计概率,从全市所有高校大一学生中随机调查![]() 人,求其中“剁手党”人数的分布列和期望.
人,求其中“剁手党”人数的分布列和期望.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,一个铝合金窗是由一个框架和部分外推窗框组成,其中框架设计如图2,其结构为上、下两栏,下栏为两个完全相同的矩形,四周框架和中间隔栏的材料为铝合金,宽均为![]() ,上栏和下栏的框内矩形高度(不含铝合金部分)比为
,上栏和下栏的框内矩形高度(不含铝合金部分)比为![]() ,此铝合金窗占用的墙面面积为
,此铝合金窗占用的墙面面积为![]() ,设该铝合金窗的宽和高分别
,设该铝合金窗的宽和高分别![]() ,
,![]() ,铝合金的透光部分的面积为
,铝合金的透光部分的面积为![]() (外推窗框遮挡光线部分忽略不计).
(外推窗框遮挡光线部分忽略不计).

(1)试用![]() ,
,![]() 表示
表示![]() ;
;
(2)若要使![]() 最大,则铝合金窗的宽和高分别为多少?
最大,则铝合金窗的宽和高分别为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com