
【题目】如图,已知椭圆![]() ,左、右焦点分别为
,左、右焦点分别为![]() ,
,![]() ,右顶点为
,右顶点为![]() ,上顶点为
,上顶点为![]() ,
,![]() 为椭圆上在第一象限内一点.
为椭圆上在第一象限内一点.
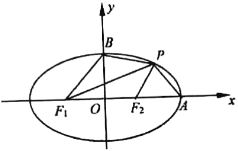
(1)若![]() .
.
①求椭圆的离心率![]() ;
;
②求直线![]() 的斜率.
的斜率.
(2)若![]() ,
,![]() ,
,![]() 成等差数列,且
成等差数列,且![]() ,求直线
,求直线![]() 的斜率的取值范围.
的斜率的取值范围.
科目:高中数学 来源: 题型:
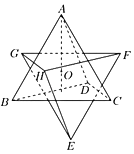
【题目】正四面体ABCD的体积为1,O为其中心,正四面体EFGH与正四面体ABCD关于点O对称,则这两个正四面体的公共部分的体积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知抛物线
中,已知抛物线![]() :
:![]() ,过抛物线焦点
,过抛物线焦点![]() 且与
且与![]() 轴垂直的直线与抛物线相交于
轴垂直的直线与抛物线相交于![]() 、
、![]() 两点,且
两点,且![]() 的周长为
的周长为![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)若过焦点![]() 且斜率为1的直线
且斜率为1的直线![]() 与抛物线
与抛物线![]() 相交于
相交于![]() 、
、![]() 两点,过点
两点,过点![]() 、
、![]() 分别作抛物线
分别作抛物线![]() 的切线
的切线![]() 、
、![]() ,切线
,切线![]() 与
与![]() 相交于点
相交于点![]() ,求:
,求:![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若曲线![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 垂直,求函数
垂直,求函数![]() 的单调区间;
的单调区间;
(2)若对于任意![]() 都有
都有![]() 成立,试求
成立,试求![]() 的取值范围;
的取值范围;
(3)记![]() .当
.当![]() 时,函数
时,函数![]() 在区间
在区间![]() 上有两个零点,求实数
上有两个零点,求实数![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
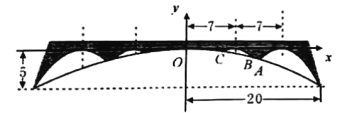
【题目】早在一千多年之前,我国已经把溢流孔用于造桥技术,以减轻桥身重量和水流对桥身的冲击,现设桥拱上有如图所示的4个溢流孔,桥拱和溢流孔轮廓线均为抛物线的一部分,且四个溢流孔轮廓线相同.根据图上尺寸,在平面直角坐标系![]() 中,桥拱所在抛物线的方程为_______,溢流孔与桥拱交点
中,桥拱所在抛物线的方程为_______,溢流孔与桥拱交点![]() 的坐标为_______.
的坐标为_______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将一个各个面上均涂有颜色的正方体锯成![]() 个同样大小的小正方体,从这些小正方体中任意取两个,这两个都恰是两面涂色的概率是( )
个同样大小的小正方体,从这些小正方体中任意取两个,这两个都恰是两面涂色的概率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】祖暅(公元前5~6世纪)是我国齐梁时代的数学家,是祖冲之的儿子,他提出了一条原原理:“幂势既同,则积不容异.”这里的“幂”指水平截面的面积,“势”指高。这句话的意思是:两个等高的几何体若在所有等高处的水平截面的面积相等,则这两个几何体体积相等。设由椭圆![]() 所围成的平面图形绕
所围成的平面图形绕![]() 轴旋转一周后,得一橄榄状的几何体(称为椭球体),课本中介绍了应用祖暅原理求球体体积公式的做法,请类比此法,求出椭球体体积,其体积等于( )
轴旋转一周后,得一橄榄状的几何体(称为椭球体),课本中介绍了应用祖暅原理求球体体积公式的做法,请类比此法,求出椭球体体积,其体积等于( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】前些年有些地方由于受到提高![]() 的影响,部分企业只重视经济效益而没有树立环保意识,把大量的污染物排放到空中与地下,严重影响了人们的正常生活,为此政府进行强制整治,对不合格企业进行关闭、整顿,另一方面进行大量的绿化来净化和吸附污染物.通过几年的整治,环境明显得到好转,针对政府这一行为,老百姓大大点赞.
的影响,部分企业只重视经济效益而没有树立环保意识,把大量的污染物排放到空中与地下,严重影响了人们的正常生活,为此政府进行强制整治,对不合格企业进行关闭、整顿,另一方面进行大量的绿化来净化和吸附污染物.通过几年的整治,环境明显得到好转,针对政府这一行为,老百姓大大点赞.
(1)某机构随机访问50名居民,这50名居民对政府的评分(满分100分)如下表:
分数 |
|
|
|
|
|
|
频数 | 2 | 3 | 11 | 14 | 11 | 9 |
请在答题卡上作出居民对政府的评分频率分布直方图:
(2)当地环保部门随机抽测了2018年11月的空气质量指数,其数据如下表:
空气质量指数( | 0-50 | 50-100 | 100-150 | 150-200 |
天数 | 2 | 18 | 8 | 2 |
用空气质量指数的平均值作为该月空气质量指数级别,求出该月空气质量指数级别为第几级?(同一组数据用该组数据的区间中点值作代表,将频率视为概率)(相关知识参见附表)
(3)空气受到污染,呼吸系统等疾病患者最易感染,根据历史经验,凡遇到空气轻度污染,小李每天会服用有关药品,花费50元,遇到中度污染每天服药的费用达到100元.环境整治前的2015年11月份小李因受到空气污染患呼吸系统等疾病花费了5000元,试估计2018年11月份(参考(2)中表格数据)小李比以前少花了多少钱的医药费?
附:
空气质量指数( | 0-50 | 50-100 | 100-150 | 150-200 | 200-300 |
|
空气质量指数级别 | Ⅰ | Ⅱ | Ⅲ | Ⅳ | Ⅴ | Ⅵ |
空气质量指数 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知棱柱![]() 的底面是菱形,且
的底面是菱形,且![]() 面ABCD,
面ABCD,![]() ,F为棱
,F为棱![]() 的中点,M为线段
的中点,M为线段![]() 的中点.
的中点.
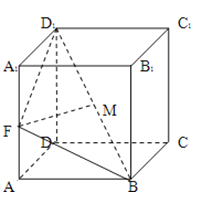
(1)求证:![]() 面ABCD;
面ABCD;
(2)判断直线MF与平面![]() 的位置关系,并证明你的结论;
的位置关系,并证明你的结论;
(3)求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com