【题目】已知抛物线的焦点为，为上位于第一象限的任意一点，过点的直线交于另一点，交轴的正半轴于点．

(1)若当点的横坐标为，且为等边三角形，求的方程；

(2)对于(1)中求出的抛物线，若点，记点关于轴的对称点为，交轴于点，且，求证：点的坐标为，并求点到直线的距离的取值范围．

【题目】四棱锥底面是菱形，平面，，分别是的中点.

（1）求证：平面平面；

（2），垂足为，斜线与平面所成的角为，求二面角的正切值.

【题目】设不等式确定的平面区域为U，确定的平面区域为V.

（1）定义横、纵坐标为整数的点为“整点”，在区域U内任取3个整点，求这些整点中恰有2个整点在区域V内的概率；

（2）设集合；集合若从集合A到集合B可以建立m个不同的映射？从集合B到集合A可以建立n个不同的映射，求m，n的值.

【题目】某种出口产品的关税税率，市场价格（单位：千元）与市场供应量（单位：万件）之间近似满足关系式：，其中、均为常数.当关税税率为时，若市场价格为5千元，则市场供应量约为1万件；当关税税率为时，若市场价格为7千元，则市场供应量约为2万件.

（1）试确定、的值；

（2）市场需求量（单位：万件）与市场价格近似满足关系式：.当时，市场价格称为市场平衡价格.当市场平衡价格不超过4千元时，试确定关税税率的最大值.

【题目】已知函数 (其中)，若点是函数图象的一个对称中心．

(1)求的解析式，并求的最小正周期；

(2)将函数的图象向左平移个单位，再将所得图象上各点的横坐标伸长为原来的倍，纵坐标不变，得到函数的图象，用 “五点作图法”作出函数在区间上的图象．

【题目】已知函数．

（1）求函数的单调区间；

（2）若函数的图象在点处的切线的斜率为1，问：在什么范围取值时，对于任意的，函数在区间上总存在极值？

【题目】宜昌大剧院和宜昌奥体中心将是人们健康生活的最佳场所，若两处在同一直角坐标系中的坐标分别为，；假设至喜长江大桥所在的直线方程为直线.现为方便大家出行，计划在至喜长江大桥上的点p处新增一出口通往两地，要使从 处到两地的总路程最短.

（1）求点p的坐标.

（2）一中高二体育特长生小陶和小陈相约某周日上午8时到9时在宜昌奥体中心会面，并约定先到者应等候另一个人一刻钟，过时即可离去，求两人能会面的概率.

【题目】在四棱锥P-ABCD中，ABCD为梯形，AB//CD，BC⊥AB，AB=2，BC=，CD=PC=。

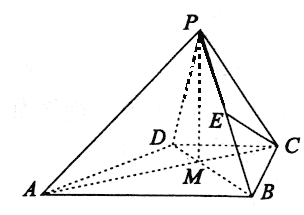
（I）点E在线段PB上，满足CE//平面PAD，求的值。

（II）已知AC与BD的交点为M，若PM=1，且平面PAC⊥平面ABCD，求二面角P-BC-M平面角的余弦值。

【题目】已知函数f（x）=|lnx|，g（x）=，则方程|f（x）+g（x）|=1实根的个数为________．

（Ⅰ）为增加趣味性，约定：每个人通过掷一枚质地均匀的骰子决定自己去参加哪个项目联欢，掷出点数为1或2的人去参加甲项目联欢，掷出点数大于2的人去参加乙项目联欢.求这5人中恰好有3人去参加甲项目联欢的概率；

（Ⅱ）若从这5人中随机选派3人去参加甲项目联欢，设表示这3个人中女生的人数，求随机变量的分布列与数学期望.