
科目: 来源: 题型:
【题目】某市一次全市高中男生身高统计调查数据显示:全市10万名男生的身高服从正态分布![]() .现从某学校高中男生中随机抽取50名测量身高,测量发现被测学生身高全部介于160cm和190cm之间,将身高的测量结果按如下方式分成5组:第1组[160,166),第2组[166,172),...,第5组[184,190]下表是按上述分组方法得到的频率分布表:
.现从某学校高中男生中随机抽取50名测量身高,测量发现被测学生身高全部介于160cm和190cm之间,将身高的测量结果按如下方式分成5组:第1组[160,166),第2组[166,172),...,第5组[184,190]下表是按上述分组方法得到的频率分布表:
分组 | [160,166) | [166,172) | [172,178) | [178,184) | [184,190] |
人数 | 3 | 10 | 24 | 10 | 3 |
这50个数据的平均数和方差分别比10万个数据的平均数和方差多1和6.68,且这50个数据的方差为![]() .(同组中的身高数据用该组区间的中点值作代表):
.(同组中的身高数据用该组区间的中点值作代表):
(1)求![]() ,
,![]() ;
;
(2)给出正态分布的数据:![]() ,
,![]() .
.
(i)若从这10万名学生中随机抽取1名,求该学生身高在(169,179)的概率;
(ii)若从这10万名学生中随机抽取1万名,记![]() 为这1万名学生中身高在(169,184)的人数,求
为这1万名学生中身高在(169,184)的人数,求![]() 的数学期望.
的数学期望.
查看答案和解析>>
科目: 来源: 题型:
【题目】假设某种人寿保险规定,投保人没活过65岁,保险公司要赔偿10万元;若投保人活过65岁,则保险公司不赔偿,但要给投保人一次性支付4万元已知购买此种人寿保险的每个投保人能活过65岁的概率都为![]() ,随机抽取4个投保人,设其中活过65岁的人数为
,随机抽取4个投保人,设其中活过65岁的人数为![]() ,保险公司支出给这4人的总金额为
,保险公司支出给这4人的总金额为![]() 万元(参考数据:
万元(参考数据:![]() )
)
(1)指出X服从的分布并写出![]() 与
与![]() 的关系;
的关系;
(2)求![]() .(结果保留3位小数)
.(结果保留3位小数)
查看答案和解析>>
科目: 来源: 题型:
【题目】某超市国庆大酬宾,购物满100元可参加一次游戏抽奖活动,游戏抽奖规则如下:顾客将一个半径适当的小球放入如图所示的容器正上方的入口处,小球自由落下过程中,将3次遇到黑色障碍物,最后落入A袋或B袋中,落入A袋得奖金4元,落入B袋得奖金8元,已知小球每次遇到黑色障碍物时,向左向右下落的概率都为![]() .已知李女士当天在该超市购物消费128元,按照活动要求,李女士的活动奖金期望值为_____元.
.已知李女士当天在该超市购物消费128元,按照活动要求,李女士的活动奖金期望值为_____元.
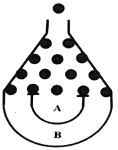
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系xOy中,己知椭圆C:![]() 的左、右顶点为A,B,右焦点为F.过点A且斜率为k(
的左、右顶点为A,B,右焦点为F.过点A且斜率为k(![]() )的直线交椭圆C于另一点P.
)的直线交椭圆C于另一点P.
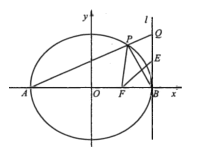
(1)求椭圆C的离心率;
(2)若![]() ,求
,求![]() 的值;
的值;
(3)设直线l:![]() ,延长AP交直线l于点Q,线段BO的中点为E,求证:点B关于直线EF的对称点在直线PF上。
,延长AP交直线l于点Q,线段BO的中点为E,求证:点B关于直线EF的对称点在直线PF上。
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,某沿海地区计划铺设一条电缆联通A,B两地,A地位于东西方向的直线MN上的陆地处,B地位于海上一个灯塔处,在A地用测角器测得![]() ,在A地正西方向4km的点C处,用测角器测得
,在A地正西方向4km的点C处,用测角器测得![]() .拟定铺设方案如下:在岸MN上选一点P,先沿线段AP在地下铺设,再沿线段PB在水下铺设.预算地下、水下的电缆铺设费用分别为2万元/km和4万元/km,设
.拟定铺设方案如下:在岸MN上选一点P,先沿线段AP在地下铺设,再沿线段PB在水下铺设.预算地下、水下的电缆铺设费用分别为2万元/km和4万元/km,设![]() ,
,![]() ,铺设电缆的总费用为
,铺设电缆的总费用为![]() 万元.
万元.
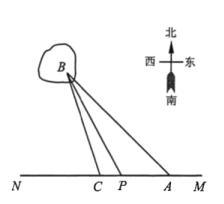
(1)求函数![]() 的解析式;
的解析式;
(2)试问点P选在何处时,铺设的总费用最少,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com