【题目】如图，在四棱锥中，底面是矩形，是的中点，平面，且，．

（1）求证：；

（2）求与平面所成角的正弦值；

（3）求二面角的余弦值．

【题目】已知椭圆的左、右焦点分别为，是椭圆上两点，是坐标原点，且，，离心率为.

（1）求椭圆的方程；

（2）过作两条相互垂直的直线分别交椭圆于和，求的取值范围.

【题目】圆锥（其中为顶点，为底面圆心）的侧面积与底面积的比是，则圆锥与它的外接球（即顶点在球面上且底面圆周也在球面上）的体积比为__________．

【题目】为迎接双流中学建校周年校庆，双流区政府计划提升双流中学办学条件.区政府联合双流中学组成工作组，与某建设公司计划进行个重点项目的洽谈，考虑到工程时间紧迫的现状，工作组对项目洽谈的顺序提出了如下要求：重点项目甲必须排在前三位，且项目丙、丁必须排在一起，则这六个项目的不同安排方案共有（）

A.种B.种C.种D.种

【题目】已知函数，且是曲线的切线.

（1）求实数a的值以及切点坐标；

（2）求证：.

【题目】已知点A，B是抛物线上关于轴对称的两点，点E是抛物线C的准线与x轴的交点.

（1）若是面积为4的直角三角形，求抛物线C的方程；

（2）若直线BE与抛物线C交于另一点D，证明：直线AD过定点.

以车辆在停车场停留时间位于各区间的频率代替车辆在停车场停留时间位于各区间的概率。

（1）X表示某辆车在该停车场停车一次所交费用，求X的概率分布列及期望；

（2）现随机抽取该停车场内停放的3辆车，表示3辆车中停车费用少于的车辆数，求的概率.

【题目】如图所示，在四棱锥中，，平面PAB，，E为线段PB的中点

（1）证明：平面PDC；

（2）求直线DE与平面PDC所成角的正弦值.

【题目】已知动圆过定点，且与直线相切.

（1）求动圆圆心的轨迹的方程；

（2）设是轨迹上异于原点的两个不同点，直线和的斜率分别为，且，证明直线恒过定点，并求出该定点的坐标

【题目】如图，椭圆C：(a＞b＞0)的离心率为，其左焦点到点P(2，1)的距离为．不过原点O的直线l与C相交于A，B两点，且线段AB被直线OP平分．

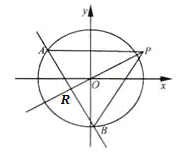
(Ⅰ)求椭圆C的方程；

(Ⅱ) 求ABP的面积取最大时直线l的方程．