
科目: 来源: 题型:
【题目】一种作图工具如图1所示.![]() 是滑槽
是滑槽![]() 的中点,短杆
的中点,短杆![]() 可绕
可绕![]() 转动,长杆
转动,长杆![]() 通过
通过![]() 处铰链与
处铰链与![]() 连接,
连接,![]() 上的栓子
上的栓子![]() 可沿滑槽AB滑动,且
可沿滑槽AB滑动,且![]() ,
,![]() .当栓子
.当栓子![]() 在滑槽AB内作往复运动时,带动
在滑槽AB内作往复运动时,带动![]() 绕
绕![]() 转动一周(
转动一周(![]() 不动时,
不动时,![]() 也不动),
也不动),![]() 处的笔尖画出的曲线记为
处的笔尖画出的曲线记为![]() .以
.以![]() 为原点,
为原点,![]() 所在的直线为
所在的直线为![]() 轴建立如图2所示的平面直角坐标系.
轴建立如图2所示的平面直角坐标系.
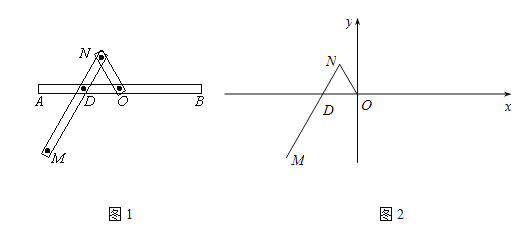
(Ⅰ)求曲线C的方程;
(Ⅱ)设动直线![]() 与两定直线
与两定直线![]() 和
和![]() 分别交于
分别交于![]() 两点.若直线
两点.若直线![]() 总与曲线
总与曲线![]() 有且只有一个公共点,试探究:
有且只有一个公共点,试探究:![]() 的面积是否存在最小值?若存在,求出该最小值;若不存在,说明理由.
的面积是否存在最小值?若存在,求出该最小值;若不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知复数z满足|z|![]() ,z的实部大于0,z2的虚部为2.
,z的实部大于0,z2的虚部为2.
(1)求复数z;
(2)设复数z,z2,z﹣z2之在复平面上对应的点分别为A,B,C,求(![]() )
)![]()
![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】为践行“绿水青山就是金山银山”的发展理念,某城区对辖区内![]() ,
,![]() ,
,![]() 三类行业共200个单位的生态环境治理成效进行了考核评估,考评分数达到80分及其以上的单位被称为“星级”环保单位,未达到80分的单位被称为“非星级”环保单位.现通过分层抽样的方法获得了这三类行业的20个单位,其考评分数如下:
三类行业共200个单位的生态环境治理成效进行了考核评估,考评分数达到80分及其以上的单位被称为“星级”环保单位,未达到80分的单位被称为“非星级”环保单位.现通过分层抽样的方法获得了这三类行业的20个单位,其考评分数如下:
![]() 类行业:85,82,77,78,83,87;
类行业:85,82,77,78,83,87;
![]() 类行业:76,67,80,85,79,81;
类行业:76,67,80,85,79,81;
![]() 类行业:87,89,76,86,75,84,90,82.
类行业:87,89,76,86,75,84,90,82.
(Ⅰ)计算该城区这三类行业中每类行业的单位个数;
(Ⅱ)若从抽取的![]() 类行业这6个单位中,再随机选取3个单位进行某项调查,求选出的这3个单位中既有“星级”环保单位,又有“非星级”环保单位的概率.
类行业这6个单位中,再随机选取3个单位进行某项调查,求选出的这3个单位中既有“星级”环保单位,又有“非星级”环保单位的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() ,
,![]() 的在数集
的在数集![]() 上都有定义,对于任意的
上都有定义,对于任意的![]() ,当
,当![]() 时,
时,![]() 或
或![]() 成立,则称
成立,则称![]() 是数集
是数集![]() 上
上![]() 的限制函数.
的限制函数.
(1)求![]() 在
在![]() 上的限制函数
上的限制函数![]() 的解析式;
的解析式;
(2)证明:如果![]() 在区间
在区间![]() 上恒为正值,则
上恒为正值,则![]() 在
在![]() 上是增函数;[注:如果
上是增函数;[注:如果![]() 在区间
在区间![]() 上恒为负值,则
上恒为负值,则![]() 在区间
在区间![]() 上是减函数,此结论无需证明,可以直接应用]
上是减函数,此结论无需证明,可以直接应用]
(3)利用(2)的结论,求函数![]() 在
在![]() 上的单调区间.
上的单调区间.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的左右焦点为
的左右焦点为![]() ,
,![]() ,
,![]() 是椭圆上半部分的动点,连接
是椭圆上半部分的动点,连接![]() 和长轴的左右两个端点所得两直线交
和长轴的左右两个端点所得两直线交![]() 正半轴于
正半轴于![]() ,
,![]() 两点(点
两点(点![]() 在
在![]() 的上方或重合).
的上方或重合).
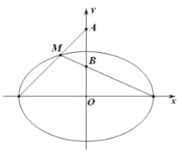
(1)当![]() 面积
面积![]() 最大时,求椭圆的方程;
最大时,求椭圆的方程;
(2)当![]() 时,若
时,若![]() 是线段
是线段![]() 的中点,求直线
的中点,求直线![]() 的方程;
的方程;
(3)当![]() 时,在
时,在![]() 轴上是否存在点
轴上是否存在点![]() 使得
使得![]() 为定值,若存在,求
为定值,若存在,求![]() 点的坐标,若不存在,说明理由.
点的坐标,若不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】对年利率为![]() 的连续复利,要在
的连续复利,要在![]() 年后达到本利和
年后达到本利和![]() ,则现在投资值为
,则现在投资值为![]() ,
,![]() 是自然对数的底数.如果项目
是自然对数的底数.如果项目![]() 的投资年利率为
的投资年利率为![]() 的连续复利.
的连续复利.
(1)现在投资5万元,写出满![]() 年的本利和,并求满10年的本利和;(精确到0.1万元)
年的本利和,并求满10年的本利和;(精确到0.1万元)
(2)一个家庭为刚出生的孩子设立创业基金,若每年初一次性给项目![]() 投资2万元,那么,至少满多少年基金共有本利和超过一百万元?(精确到1年)
投资2万元,那么,至少满多少年基金共有本利和超过一百万元?(精确到1年)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知直线l:x![]() y
y![]() 2=0,抛物线C:y2=2px(p>0).
2=0,抛物线C:y2=2px(p>0).
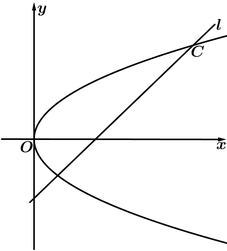
(1)若直线l过抛物线C的焦点,求抛物线C的方程;
(2)已知抛物线C上存在关于直线l对称的相异两点P和Q.
①求证:线段PQ的中点坐标为![]() ;
;
②求p的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】在线段![]() 的两端点各置一个光源,已知光源
的两端点各置一个光源,已知光源![]() ,
,![]() 的发光强度之比为
的发光强度之比为![]() ,则线段上光照度最小的一点到
,则线段上光照度最小的一点到![]() ,
,![]() 的距离之比为______(光学定律:
的距离之比为______(光学定律:![]() 点的光照度与
点的光照度与![]() 到光源的距离的平方成反比,与光源的发光强度成正比)
到光源的距离的平方成反比,与光源的发光强度成正比)
查看答案和解析>>
科目: 来源: 题型:
【题目】已知三棱锥![]() (如图1)的平面展开图(如图2)中,四边形
(如图1)的平面展开图(如图2)中,四边形![]() 为边长为
为边长为![]() 的正方形,△ABE和△BCF均为正三角形,在三棱锥
的正方形,△ABE和△BCF均为正三角形,在三棱锥![]() 中:
中:
(I)证明:平面![]()
![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值;
的余弦值;
(Ⅲ)若点![]() 在棱
在棱![]() 上,满足
上,满足![]() ,
, ![]() ,点
,点![]() 在棱
在棱![]() 上,且
上,且![]() ,求
,求![]() 的取值范围.
的取值范围.

查看答案和解析>>
科目: 来源: 题型:
【题目】由A,B,C,…等7人担任班级的7个班委.
(1)若正、副班长两职只能由A,B,C这三人中选两人担任,则有多少种分工方案?
(2)若正、副班长两职至少要选A,B,C这三人中的1人担任,有多少种分工方案?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com