【题目】设函数

（1）若函数在上递增，在上递减，求实数的值.

（2））讨论在上的单调性；

（3）若方程有两个不等实数根，求实数的取值范围，并证明.

【题目】为了适应高考改革，某中学推行“创新课堂”教学．高一平行甲班采用“传统教学”的教学方式授课，高一平行乙班采用“创新课堂”的教学方式授课，为了比较教学效果，期中考试后，分别从两个班中各随机抽取名学生的成绩进行统计分析，结果如下表：（记成绩不低于分者为“成绩优秀”）

（Ⅰ）由以上统计数据填写下面的列联表，并判断是否有以上的把握认为“成绩优秀与教学方式有关”？

（Ⅱ）现从上述样本“成绩不优秀”的学生中，抽取人进行考核，记“成绩不优秀”的乙班人数为，求的分布列和期望．

参考公式：，其中．

临界值表

A.命题“”的否定是“”

B.命题“已知，若则或”是真命题

C.命题“若则函数只有一个零点”的逆命题为真命题

D.“在上恒成立”在上恒成立

【题目】定义在上的函数，单调递增，，若对任意，存在，使得成立，则称是在上的“追逐函数”.若，则下列四个命题：①是在上的“追逐函数”；②若是在上的“追逐函数”，则；③是在上的“追逐函数”；④当时，存在，使得是在上的“追逐函数”.其中正确命题的个数为（ ）

A. ①③B. ②④C. ①④D. ②③

【题目】海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比，收获时各随机抽取了个网箱，测量各水箱产品的产量（单位：kg），其频率分布直方图如下图所示.

（1）若用频率视为概率，记表示事件“旧养殖法的箱产量低于kg”，求事件的概率；

（2）填写以下列联表，并根据此判断是否有的把握认为箱产量与养殖方法有关？

（3）根据箱产量频率分布直方图，求新养殖法箱产量的中位数的估计值（精确到）

从这20天中随机选取一天，随机变量X表示在维修处该天元件A的维修个数．

（Ⅰ）求X的分布列与数学期望；

（Ⅱ）若a，b，且b-a=6，求最大值；

（Ⅲ）目前维修处有两名工人从事维修工作，为使每个维修工人每天维修元件A的个数的数学期望不超过4个，至少需要增加几名维修工人？（只需写出结论）

【题目】已知如图1，在Rt△ABC中，∠ACB=30°，∠ABC=90°，D为AC中点，AEBD于E，延长AE交BC于F，将△ABD沿BD折起，使平面ABD平面BCD，如图2所示。

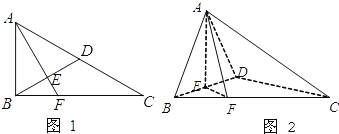
（Ⅰ）求证：AE平面BCD；

（Ⅱ）求二面角A-DC-B的余弦值；

（Ⅲ）求三棱锥B-AEF与四棱锥A-FEDC的体积的比（只需写出结果，不要求过程）．

【题目】已知函数，函数.

（1）求函数在上的最小值；

（2）函数，若在其定义域内有两个不同的极值点，求a的取值范围；

（3）记的两个极值点分别为，且.已知，若不等式恒成立，求的取值范围.注：为自然对数的底数.

【题目】单位正方体ABCD-，黑、白两蚂蚁从点A出发沿棱向前爬行，每走完一条棱称为“走完一段”．白蚂蚁爬地的路线是AA1→A1D1→‥，黑蚂蚁爬行的路线是AB→BB1→‥，它们都遵循如下规则：所爬行的第i+2段与第i段所在直线必须是异面直线（iN*）.设白、黑蚂蚁都走完2020段后各自停止在正方体的某个顶点处，这时黑、白两蚂蚁的距离是（ ）

A.1B.C.D.0

【题目】已知抛物线经过点，过A作两条不同直线，其中直线关于直线对称.

（1）求抛物线E的方程及其准线方程；

（2）设直线分别交抛物线E于两点（均不与A重合），若以线段为直径的圆与抛物线E的准线相切，求直线的方程.