
科目: 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() ,(
,(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出曲线![]() 的极坐标方程和曲线
的极坐标方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若射线![]() 与曲线
与曲线![]() 相交于点
相交于点![]() ,将
,将![]() 逆时针旋转
逆时针旋转![]() 后,与曲线
后,与曲线![]() 相交于点
相交于点![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】甲乙两个班级均为 40 人,进行一门考试后,按学生考试成绩及格与不及格进行统计,甲班及格人数为 36 人,乙班及格人数为 24 人.
(1)根据以上数据建立一个2![]() 2的列联表;
2的列联表;
(2)试判断是否成绩与班级是否有关?
参考公式:![]() ;
;![]()
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.84 | 5.024 | 6.635 | 7.879 | 10.83 |
查看答案和解析>>
科目: 来源: 题型:
【题目】绝大部分人都有患呼吸系统疾病的经历,现在我们调查患呼吸系统疾病是否和所处环境有关.一共调查了![]() 人,患有呼吸系统疾病的
人,患有呼吸系统疾病的![]() 人,其中
人,其中![]() 人在室外工作,
人在室外工作,![]() 人在室内工作.没有患呼吸系统疾病的
人在室内工作.没有患呼吸系统疾病的![]() 人,其中
人,其中![]() 人在室外工作,
人在室外工作,![]() 人在室内工作.
人在室内工作.
(1)现采用分层抽样从室内工作的居民中抽取一个容量为![]() 的样本,将该样本看成一个总体,从中随机的抽取两人,求两人都有呼吸系统疾病的概率.
的样本,将该样本看成一个总体,从中随机的抽取两人,求两人都有呼吸系统疾病的概率.
(2)你能否在犯错误率不超过![]() 的前提下认为感染呼吸系统疾病与工作场所有关;
的前提下认为感染呼吸系统疾病与工作场所有关;
附表:
|
|
|
|
|
|
|
|
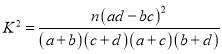
查看答案和解析>>
科目: 来源: 题型:
【题目】每个国家对退休年龄都有不一样的规定,从2018年开始我国关于延迟退休的话题一直在网上热议,为了了解市民对“延迟退休”的态度,现从某地市民中随机选取100人进行调查,调查情况如下表:
年龄段(单位:岁) |
|
|
|
|
|
|
被调查的人数 |
|
|
|
|
|
|
赞成的人数 |
|
|
|
|
|
|
(1)从赞成“延迟退休”的人中任选1人,此人年龄在![]() 的概率为
的概率为![]() ,求出表格中
,求出表格中![]() 的值;
的值;
(2)在被调查的人中,年龄低于35岁的人可以认为“低龄人”,年龄不低于35岁的人可以认为“非低龄人”,试作出是否赞成“延迟退休”与“低龄与否”的![]() 列联表,并指出有无
列联表,并指出有无![]() 的把握认为是否赞成“延迟退休”与“低龄与否”有关,并说明理由.
的把握认为是否赞成“延迟退休”与“低龄与否”有关,并说明理由.
附:![]() .
.
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系xOy中,A(﹣2,0),B(2,0),P为不在x轴上的动点,直线PA,PB的斜率满足kPAkPB![]() .
.
(1)求动点P的轨迹Γ的方程;
(2)若M,N是轨迹Γ上两点,kMN=1,求△OMN面积的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】十二生肖是十二地支的形象化代表,即子(鼠)、丑(牛)、寅(虎)、卯(兔)、辰(龙)、巳(蛇)、午(马)、未(羊)、申(猴)、酉(鸡)、戌(狗)、亥(猪),每一个人的出生年份对应了十二种动物中的一种,即自己的属相.现有印着六种不同生肖图案(包含马、羊)的毛绒娃娃各一个,小张同学的属相为马,小李同学的属相为羊,现在这两位同学从这六个毛绒娃娃中各随机取一个(不放回),则这两位同学都拿到自己属相的毛绒娃娃的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com