
科目: 来源: 题型:
【题目】给出下列结论:在回归分析中
(1)可用相关指数![]() 的值判断模型的拟合效果,
的值判断模型的拟合效果,![]() 越大,模型的拟合效果越好;
越大,模型的拟合效果越好;
(2)可用残差平方和判断模型的拟合效果,残差平方和越大,模型的拟合效果越好;
(3)可用相关系数![]() 的值判断模型的拟合效果,
的值判断模型的拟合效果,![]() 越大,模型的拟合效果越好;
越大,模型的拟合效果越好;
(4)可用残差图判断模型的拟合效果,残差点比较均匀地落在水平的带状区域中,说明这样的模型比较合适.带状区域的宽度越窄,说明模型的拟合精度越高.
以上结论中,不正确的是( )
A.(1)(3)B.(2)(3)C.(1)(4)D.(3)(4)
查看答案和解析>>
科目: 来源: 题型:
【题目】某工厂有两台不同机器![]() 和
和![]() 生产同一种产品各
生产同一种产品各![]() 万件,现从各自生产的产品中分别随机抽取
万件,现从各自生产的产品中分别随机抽取![]() 件,进行品质鉴定,鉴定成绩的茎叶图如图所示:
件,进行品质鉴定,鉴定成绩的茎叶图如图所示:
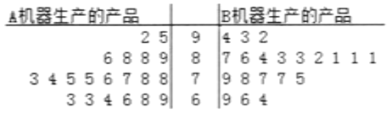
该产品的质量评价标准规定:鉴定成绩达到![]() 的产品,质量等级为优秀;鉴定成绩达到
的产品,质量等级为优秀;鉴定成绩达到![]() 的产品,质量等级为良好;鉴定成绩达到
的产品,质量等级为良好;鉴定成绩达到![]() 的产品,质量等级为合格.将这组数据的频率视为整批产品的概率.
的产品,质量等级为合格.将这组数据的频率视为整批产品的概率.
(1)完成下列![]() 列联表,以产品等级是否达到良好以上(含良好)为判断依据,判断能不能在误差不超过
列联表,以产品等级是否达到良好以上(含良好)为判断依据,判断能不能在误差不超过![]() 的情况下,认为
的情况下,认为![]() 机器生产的产品比
机器生产的产品比![]() 机器生产的产品好;
机器生产的产品好;
|
| 合计 | |
良好以上(含良好) | |||
合格 | |||
合计 |
(![]() 和
和![]() 生产的产品中各随机抽取
生产的产品中各随机抽取![]() 件,求
件,求![]() 件产品中
件产品中![]() 机器生产的优等品的数量多于
机器生产的优等品的数量多于![]() 机器生产的优等品的数量的概率;
机器生产的优等品的数量的概率;
(3)已知优秀等级产品的利润为![]() 元/件,良好等级产品的利润为
元/件,良好等级产品的利润为![]() 元/件,合格等级产品的利润为
元/件,合格等级产品的利润为![]() 元/件,
元/件,![]() 机器每生产
机器每生产![]() 万件的成本为
万件的成本为![]() 万元,
万元,![]() 机器每生产
机器每生产![]() 万件的成本为
万件的成本为![]() 万元;该工厂决定:按样本数据测算,若收益之差不超过
万元;该工厂决定:按样本数据测算,若收益之差不超过![]() 万元,则仍然保留原来的两台机器.你认为该工厂会仍然保留原来的两台机器吗?
万元,则仍然保留原来的两台机器.你认为该工厂会仍然保留原来的两台机器吗?
附:1.独立性检验计算公式: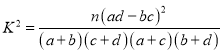 .
.
2.临界值表:
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目: 来源: 题型:
【题目】《周髀算经》 是我国古代的天文学和数学著作。其中一个问题的大意为:一年有二十四个节气(如图),每个节气晷长损益相同(即物体在太阳的照射下影子长度的增加量和减少量相同).若冬至晷长一丈三尺五寸,夏至晷长一尺五寸(注:ー丈等于十尺,一尺等于十寸),则立冬节气的晷长为( )
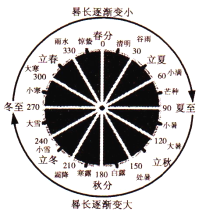
A. 九尺五寸 B. 一丈五寸 C. 一丈一尺五寸 D. 一丈六尺五寸
查看答案和解析>>
科目: 来源: 题型:
【题目】为迎接国庆汇演,学校拟对参演的班级进行奖励性加分表彰,每选中一个节目,其班级量化考核积分加3分.某班级准备了三个文娱节目,这三个节目被选中的概率分别为![]() ,
,![]() ,
,![]() ,且每个节目是否被选中是相互独立的.
,且每个节目是否被选中是相互独立的.
(1)求该班级被加分的概率;
(2)求该班级获得奖励性积分![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目: 来源: 题型:
【题目】某市在精准扶贫和生态文明建设的专项工作中,为改善农村生态环境,建设美丽乡村,开展农村生活用水排污管道“村村通”.已知排污管道外径为1米,当两条管道并行经过一块农田时,如图,要求两根管道最近距离不小于0.25米,埋没的最小覆土厚度(路面至管顶)不低于0.5米.埋设管道前先挖掘一条横截面为等腰梯形的沟渠,且管道所在的两圆分别与两腰相切.设![]() .
.

(1)为了减少农田的损毁,则当![]() 为何值时,挖掘的土方量最少?
为何值时,挖掘的土方量最少?
(2)水管用吊车放入渠底前需了解吊绳的长度,在(1)的条件下计算![]() 长度.
长度.
查看答案和解析>>
科目: 来源: 题型:
【题目】实验中学从高二级部中选拔一个班级代表学校参加“学习强国知识大赛”,经过层层选拔,甲、乙两个班级进入最后决赛,规定回答1个相关问题做最后的评判选择由哪个班级代表学校参加大赛.每个班级6名选手,现从每个班级6名选手中随机抽取3人回答这个问题已知这6人中,甲班级有4人可以正确回答这道题目,而乙班级6人中能正确回答这道题目的概率每人均为![]() ,甲、乙两班级每个人对问题的回答都是相互独立,互不影响的.
,甲、乙两班级每个人对问题的回答都是相互独立,互不影响的.
(1)求甲、乙两个班级抽取的6人都能正确回答的概率;
(2)分别求甲、乙两个班级能正确回答题目人数的期望![]() 和方差
和方差![]() 、
、![]() ,并由此分析由哪个班级代表学校参加大赛更好?
,并由此分析由哪个班级代表学校参加大赛更好?
查看答案和解析>>
科目: 来源: 题型:
【题目】在直角坐标系![]() 中,椭圆
中,椭圆![]() 经过点
经过点![]() ,右焦点
,右焦点![]() 到右准线和左顶点的距离相等,经过点
到右准线和左顶点的距离相等,经过点![]() 的直线
的直线![]() 交椭圆于点
交椭圆于点![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)点![]() 是直线
是直线![]() 上在椭圆外的一点,且
上在椭圆外的一点,且![]() ,证明:点
,证明:点![]() 在定直线上.
在定直线上.
查看答案和解析>>
科目: 来源: 题型:
【题目】下列说法中,正确的有______.
①回归直线![]() 恒过点
恒过点![]() ,且至少过一个样本点;
,且至少过一个样本点;
②根据![]() 列列联表中的数据计算得出
列列联表中的数据计算得出![]() ,而
,而![]() ,则有
,则有![]() 的把握认为两个分类变量有关系,即有
的把握认为两个分类变量有关系,即有![]() 的可能性使得“两个分类变量有关系”的推断出现错误;
的可能性使得“两个分类变量有关系”的推断出现错误;
③![]() 是用来判断两个分类变量是否相关的随机变量,当
是用来判断两个分类变量是否相关的随机变量,当![]() 的值很小时可以推断两类变量不相关;
的值很小时可以推断两类变量不相关;
④某项测量结果![]() 服从正态分布
服从正态分布![]() ,则
,则![]() ,则
,则![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】随着我国经济的发展,居民收入逐年增长.某地区2014年至2018年农村居民家庭人均纯收入![]() (单位:千元)的数据如下表:
(单位:千元)的数据如下表:
年份 | 2014 | 2015 | 2016 | 2017 | 2018 |
年份代号 | 1 | 2 | 3 | 4 | 5 |
人均纯收入 | 5 | 4 | 7 | 8 | 10 |
(1)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)利用(1)中的回归方程,分析2014年至2018年该地区农村居民家庭人均纯收入的变化情况,并预测2019年该地区农村居民家庭人均纯收入为多少?
附:回归直线的斜率和截距的最小二乘估计公式分别为 ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com