
科目: 来源: 题型:
【题目】设n为正整数,称n×n的方格表Tn的网格线的交点(共(n+1)2个交点)为格点.现将数1,2,……,(n+1)2分配给Tn的所有格点,使不同的格点分到不同的数.称Tn的一个1×1格子S为“好方格”,如果从2S的某个顶点起按逆时针方向读出的4个顶点上的数依次递增(如图是将数1,2,…,9分配给T2的格点的一种方式,其中B、C是好方格,而A、D不是好方格)设Tn中好方格个数的最大值为f(n).
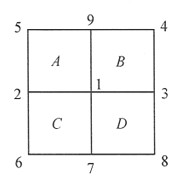
(1)求f(2)的值;
(2)求f(n)关于正整数n的表达式.
查看答案和解析>>
科目: 来源: 题型:
【题目】设a是实数,关于z的方程(z2-2z+5)(z2+2az+1)=0有4个互不相等的根,它们在复平面上对应的4个点共圆,则实数a的取值范围是________.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,设抛物线C1:![]() 的准线1与x轴交于椭圆C2:
的准线1与x轴交于椭圆C2:![]() 的右焦点F2,F1为C2的左焦点.椭圆的离心率为
的右焦点F2,F1为C2的左焦点.椭圆的离心率为![]() ,抛物线C1与椭圆C2交于x轴上方一点P,连接PF1并延长其交C1于点Q,M为C1上一动点,且在P,Q之间移动.
,抛物线C1与椭圆C2交于x轴上方一点P,连接PF1并延长其交C1于点Q,M为C1上一动点,且在P,Q之间移动.

(1)当![]() 取最小值时,求C1和C2的方程;
取最小值时,求C1和C2的方程;
(2)若△PF1F2的边长恰好是三个连续的自然数,当△MPQ面积取最大值时,求面积最大值以及此时直线MP的方程.
查看答案和解析>>
科目: 来源: 题型:
【题目】在“挑战不可能”的电视节目上,甲、乙、丙三个人组成的解密团队参加一项解密挑战活动,规则是由密码专家给出题目,然后由3个人依次出场解密,每人限定时间是1分钟内,否则派下一个人.3个人中只要有一人解密正确,则认为该团队挑战成功,否则挑战失败.根据甲以往解密测试情况,抽取了甲100次的测试记录,绘制了如图所示的频率分布直方图.
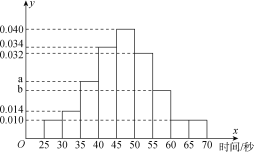
(1)若甲解密成功所需时间的中位数为47,求![]() 、
、![]() 的值,并求出甲在1分钟内解密成功的频率;
的值,并求出甲在1分钟内解密成功的频率;
(2)在“挑战不可能”节目上由于来自各方及自身的心理压力,甲,乙,丙解密成功的概率分别为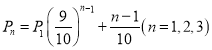 ,其中
,其中![]() 表示第
表示第![]() 个出场选手解密成功的概率,并且
个出场选手解密成功的概率,并且![]() 定义为甲抽样中解密成功的频率代替,各人是否解密成功相互独立.
定义为甲抽样中解密成功的频率代替,各人是否解密成功相互独立.
①求该团队挑战成功的概率;
②该团队以![]() 从小到大的顺序按排甲、乙、丙三个人上场解密,求团队挑战成功所需派出的人数
从小到大的顺序按排甲、乙、丙三个人上场解密,求团队挑战成功所需派出的人数![]() 的可能值及其概率.
的可能值及其概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】某小商品生产厂家计划每天生产![]() 型、
型、![]() 型、
型、![]() 型三种小商品共100个,生产一个
型三种小商品共100个,生产一个![]() 型小商品需5分钟,生产一个
型小商品需5分钟,生产一个![]() 型小商品需7分钟,生产一个
型小商品需7分钟,生产一个![]() 型小商品需4分钟,已知总生产时间不超过10小时.若生产一个
型小商品需4分钟,已知总生产时间不超过10小时.若生产一个![]() 型小商品可获利润8元,生产一个
型小商品可获利润8元,生产一个![]() 型小商品可获利润9元,生产一个
型小商品可获利润9元,生产一个![]() 型小商品可获利润6元.该厂家合理分配生产任务使每天的利润最大,则最大日利润是__________元.
型小商品可获利润6元.该厂家合理分配生产任务使每天的利润最大,则最大日利润是__________元.
查看答案和解析>>
科目: 来源: 题型:
【题目】![]() 年
年![]() 月
月![]() 日,国务院总理李克强在做政府工作报告时说,打好精准脱贫攻坚战.江西省贫困县脱贫摘帽取得突破性进展:
日,国务院总理李克强在做政府工作报告时说,打好精准脱贫攻坚战.江西省贫困县脱贫摘帽取得突破性进展:![]() 年,稳定实现扶贫对象“两不愁、三保障”,贫困县全部退出.围绕这个目标,江西正着力加快增收步伐,提高救助水平,改善生活条件,打好产业扶贫、保障扶贫、安居扶贫三场攻坚战.为响应国家政策,老张自力更生开了一间小型杂货店.据长期统计分析,老张的杂货店中某货物每天的需求量
年,稳定实现扶贫对象“两不愁、三保障”,贫困县全部退出.围绕这个目标,江西正着力加快增收步伐,提高救助水平,改善生活条件,打好产业扶贫、保障扶贫、安居扶贫三场攻坚战.为响应国家政策,老张自力更生开了一间小型杂货店.据长期统计分析,老张的杂货店中某货物每天的需求量![]() 在
在![]() 与
与![]() 之间,日需求量
之间,日需求量![]() (件)的频率
(件)的频率![]() 分布如下表所示:
分布如下表所示:
![]()
己知其成本为每件![]() 元,售价为每件
元,售价为每件![]() 元若供大于求,则每件需降价处理,处理价每件
元若供大于求,则每件需降价处理,处理价每件![]() 元.
元.
(1)设每天的进货量为![]() ,视日需求量
,视日需求量![]() 的频率为概率
的频率为概率![]() ,求在每天进货量为
,求在每天进货量为![]() 的条件下,日销售量
的条件下,日销售量![]() 的期望值
的期望值![]() (用
(用![]() 表示);
表示);
(2)在(1)的条件下,写出![]() 和
和![]() 的关系式,并判断
的关系式,并判断![]() 为何值时,日利润的均值最大.
为何值时,日利润的均值最大.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知![]()
(1)求![]() 的轨迹
的轨迹![]()
(2)过轨迹![]() 上任意一点
上任意一点![]() 作圆
作圆![]() 的切线
的切线![]() ,设直线
,设直线![]() 的斜率分别是
的斜率分别是![]() ,试问在三个斜率都存在且不为0的条件下,
,试问在三个斜率都存在且不为0的条件下, 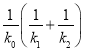 是否是定值,请说明理由,并加以证明.
是否是定值,请说明理由,并加以证明.
查看答案和解析>>
科目: 来源: 题型:
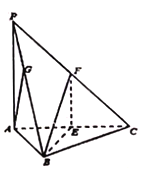
【题目】如图,在三棱锥![]() 中,底面是边长为4的正三角形,
中,底面是边长为4的正三角形,![]() ,
,![]() 底面
底面![]() ,点
,点![]() 分别为
分别为![]() ,
,![]() 的中点.
的中点.
(1)求证:平面![]() 平面
平面![]() ;
;
(2)在线段![]() 上是否存在点
上是否存在点![]() ,使得直线
,使得直线![]() 与平面
与平面![]() 所成的角的正弦值为
所成的角的正弦值为![]() ?若存在,确定点
?若存在,确定点![]() 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com