【题目】为丰富学生课外生活，某市组织了高中生钢笔书法比赛，比赛分两个阶段进行：第一阶段由评委给出所有参赛作品评分，并确定优胜者；第二阶段为附加赛，参赛人员由组委会按规则另行确定.数据统计员对第一阶段的分数进行了统计分析，这些分数都在内，在以组距为5画分数的频率分布直方图（设“”)时，发现满足.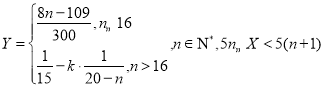

（1）试确定的所有取值，并求；

（2）组委会确定：在第一阶段比赛中低于85分的参赛者无缘获奖也不能参加附加赛；分数在的参赛者评为一等奖；分数在的同学评为二等奖，但通过附加赛有的概率提升为一等奖；分数在的同学评为三等奖，但通过附加赛有的概率提升为二等奖（所有参加附加赛的获奖人员均不降低获奖等级）.已知学生和均参加了本次比赛，且学生在第一阶段评为二等奖.

（）求学生最终获奖等级不低于学生的最终获奖等级的概率；

（）已知学生和都获奖，记两位同学最终获得一等奖的人数为，求的分布列和数学期望.

【题目】已知椭圆与抛物线有共同的焦点，且两曲线的公共点到的距离是它到直线 （点在此直线右侧）的距离的一半.

（1）求椭圆的方程；

（2）设为坐标原点，直线过点且与椭圆交于两点，以为邻边作平行四边形.是否存在直线，使点落在椭圆或抛物线上？若存在，求出点坐标；若不存在，请说明理由.

【题目】在如图的空间几何体中，四边形为直角梯形，，，，且平面平面，为棱中点.

（1）证明：；

（2）求二面角的正弦值.

【题目】设函数恰有两个极值点，则实数的取值范围是( )

A.B.

C.D.

【题目】已知函数在区间上有且仅有2个零点，对于下列4个结论：①在区间上存在，满足；②在区间有且仅有1个最大值点；③在区间上单调递增；④的取值范围是，其中所有正确结论的编号是( )

A.①③B.①③④C.②③D.①④

A.若“”为真命题，则“”为真命题

B.命题“”的否定是“”

C.命题“若，则”的逆否命题为真命题

D.“”是“”的必要不充分条件

【题目】在平面直角坐标系中，的参数方程为（t为参数）.以坐标原点O为极点，x轴的正半轴为极轴建立极坐标系，曲线C的极坐标方程为.

（1）求的普通方程和曲线C的直角坐标方程；

（2）求曲线C上的点到距离的最大值及该点坐标.

【题目】如下面左图，在直角梯形中，，，，，，点在上，且，将沿折起，得到四棱锥（如下面右图）.

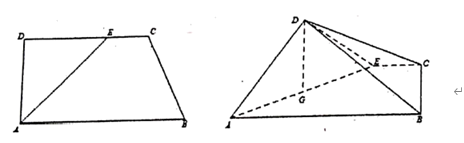
（1）求四棱锥的体积的最大值；

（2）在线段上是否存在点，使得平面？若存在，求的值；若不存在，请说明理由.

【题目】已知四面体的棱长满足，，现将四面体放入一个主视图为等边三角形的圆锥中，使得四面体可以在圆锥中任意转动，则圆锥侧面积的最小值为___________.