
科目: 来源: 题型:
【题目】学校艺术节对![]() 四件参赛作品只评一件一等奖,在评奖揭晓前,甲,乙,丙,丁四位同学对这四件参赛作品预测如下:
四件参赛作品只评一件一等奖,在评奖揭晓前,甲,乙,丙,丁四位同学对这四件参赛作品预测如下:
甲说:“是![]() 或
或![]() 作品获得一等奖”; 乙说:“
作品获得一等奖”; 乙说:“ ![]() 作品获得一等奖”;
作品获得一等奖”;
丙说:“ ![]() 两件作品未获得一等奖”; 丁说:“是
两件作品未获得一等奖”; 丁说:“是![]() 作品获得一等奖”.
作品获得一等奖”.
评奖揭晓后,发现这四位同学中只有两位说的话是对的,则获得一等奖的作品是_________.
查看答案和解析>>
科目: 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程
的参数方程 (
(![]() 为参数),直线
为参数),直线![]() 的参数方程
的参数方程 (
(![]() 为参数).
为参数).
(1)求曲线![]() 在直角坐标系中的普通方程;
在直角坐标系中的普通方程;
(2)以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,当曲线
轴的正半轴为极轴建立极坐标系,当曲线![]() 截直线
截直线![]() 所得线段的中点极坐标为
所得线段的中点极坐标为![]() 时,求直线
时,求直线![]() 的倾斜角.
的倾斜角.
查看答案和解析>>
科目: 来源: 题型:
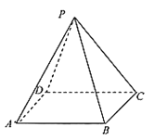
【题目】已知正四棱锥![]() 的底面边长和高都为2.现从该棱锥的5个顶点中随机选取3个点构成三角形,设随机变量
的底面边长和高都为2.现从该棱锥的5个顶点中随机选取3个点构成三角形,设随机变量![]() 表示所得三角形的面积.
表示所得三角形的面积.
(1)求概率![]() 的值;
的值;
(2)求随机变量![]() 的概率分布及其数学期望
的概率分布及其数学期望![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】某班主任对全班30名男生进行了作业量多少的调查,数据如下表:
认为作业多 | 认为作业不多 | 总计 | |
喜欢玩电脑游戏 | 12 | 8 | 20 |
不喜欢玩电脑游戏 | 2 | 8 | 10 |
总计 | 14 | 16 | 30 |
该班主任据此推断男生认为作业多与喜欢玩电脑游戏有关系,则这种推断犯错误的概率不超过________.
附表及公式:
P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式:K2=![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() .点
.点![]() 在椭圆
在椭圆![]() 上,点
上,点![]() ,
,![]() ,
,![]() 的面积为
的面积为![]() ,
,![]() 为坐标原点.
为坐标原点.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
,![]() 两点,直线
两点,直线![]() 的斜率为
的斜率为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,且
,且![]() ,证明:
,证明:![]() 的面积是定值,并求此定值.
的面积是定值,并求此定值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,三棱柱![]() 中,
中,![]() 侧面
侧面![]() ,已知
,已知![]() ,
,![]() ,
,![]() ,点E是棱
,点E是棱![]() 的中点.
的中点.

(1)求证:![]() 平面ABC;
平面ABC;
(2)在棱CA上是否存在一点M,使得EM与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】为迎接“五一国际劳动节”,某商场规定购买超过6000元商品的顾客可以参与抽奖活动现有甲品牌和乙品牌的扫地机器人作为奖品,从这两种品牌的扫地机器人中各随机抽取6台检测它们充满电后的工作时长相关数据见下表(工作时长单位:分)
机器序号 | 1 | 2 | 3 | 4 | 5 | 6 |
甲品牌工作时长/分 | 220 | 180 | 210 | 220 | 200 | 230 |
乙品牌工作时长/分 | 200 | 190 | 240 | 230 | 220 | 210 |
(1)根据所提供的数据,计算抽取的甲品牌的扫地机器人充满电后工作时长的平均数与方差;
(2)从乙品牌被抽取的6台扫地机器人中随机抽出3台扫地机器人,记抽出的扫地机器人充满电后工作时长不低于220分钟的台数为![]() ,求
,求![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,CM,CN为某公园景观湖胖的两条木栈道,∠MCN=120°,现拟在两条木栈道的A,B处设置观景台,记BC=a,AC=b,AB=c(单位:百米)
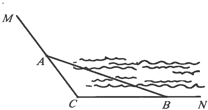
(1)若a,b,c成等差数列,且公差为4,求b的值;
(2)已知AB=12,记∠ABC=θ,试用θ表示观景路线A-C-B的长,并求观景路线A-C-B长的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com