
科目: 来源: 题型:
【题目】如图,![]() 是正方形,点
是正方形,点![]() 在以
在以![]() 为直径的半圆弧上(
为直径的半圆弧上(![]() 不与
不与![]() ,
,![]() 重合),
重合),![]() 为线段
为线段![]() 的中点,现将正方形
的中点,现将正方形![]() 沿
沿![]() 折起,使得平面
折起,使得平面![]() 平面
平面![]() .
.

(1)证明:![]() 平面
平面![]() .
.
(2)若![]() ,当三棱锥
,当三棱锥![]() 的体积最大时,求
的体积最大时,求![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
科目: 来源: 题型:
【题目】某校高三(1)班在一次语文测试结束后,发现同学们在背诵内容方面失分较为严重.为了提升背诵效果,班主任倡议大家在早晩读时间站起来大声诵读,为了解同学们对站起来大声诵读的态度,对全班50名同学进行调查,将调查结果进行整理后制成如表:
考试分数 |
|
|
|
|
|
|
频数 | 5 | 10 | 15 | 5 | 10 | 5 |
赞成人数 | 4 | 6 | 9 | 3 | 6 | 4 |
(1)欲使测试优秀率为![]() ,则优秀分数线应定为多少分?
,则优秀分数线应定为多少分?
(2)依据第1问的结果及样本数据研究是否赞成站起来大声诵读的态度与考试成绩是否优秀的关系,列出2×2列联表,并判断是否有![]() 的把握认为赞成与否的态度与成绩是否优秀有关系.
的把握认为赞成与否的态度与成绩是否优秀有关系.
参考公式及数据: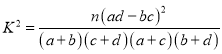 ,
,![]() .
.
| 0.100 | 0.050 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目: 来源: 题型:
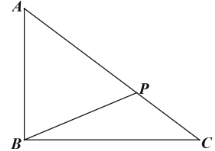
【题目】如图,在三棱锥A﹣BCD中,点E在BD上,EA=EB=EC=ED,BD![]() CD,△ACD为正三角形,点M,N分别在AE,CD上运动(不含端点),且AM=CN,则当四面体C﹣EMN的体积取得最大值
CD,△ACD为正三角形,点M,N分别在AE,CD上运动(不含端点),且AM=CN,则当四面体C﹣EMN的体积取得最大值![]() 时,三棱锥A﹣BCD的外接球的表面积为_____.
时,三棱锥A﹣BCD的外接球的表面积为_____.

查看答案和解析>>
科目: 来源: 题型:
【题目】南宋数学家杨辉在《详解九章算法》和《算法通变本末》中,提出了一些新的垛积公式,所讨论的高阶等差数列与一般等差数列不同,前后两项之差并不相等,但是逐项差数之差或者高次差成等差数列对这类高阶等差数列的研究,在杨辉之后一般称为“垛积术”.现有高阶等差数列,其前7项分别为1,4,8,14,23,36,54,则该数列的第19项为( )(注:![]() )
)
A.1624B.1024C.1198D.1560
查看答案和解析>>
科目: 来源: 题型:
【题目】已知![]() ,数列
,数列![]() 中的每一项均在集合
中的每一项均在集合![]() 中,且任意两项不相等,又对于任意的整数
中,且任意两项不相等,又对于任意的整数![]() ,均有
,均有![]() .例如
.例如![]() 时,数列
时,数列![]() 为
为![]() 或
或![]() .
.
(1)当![]() 时,试求满足条件的数列
时,试求满足条件的数列![]() 的个数;
的个数;
(2)当![]() ,求所有满足条件的数列
,求所有满足条件的数列![]() 的个数.
的个数.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知直线
中,已知直线![]() 的参数方程:
的参数方程: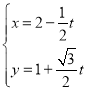 (
(![]() 为参数),以原点为极点,
为参数),以原点为极点,![]() 轴非负半轴为极轴(取相同单位长度)建立极坐标系,圆
轴非负半轴为极轴(取相同单位长度)建立极坐标系,圆![]() 的极坐标方程为:
的极坐标方程为:![]() .
.
(1)将直线![]() 的参数方程化为普通方程,圆
的参数方程化为普通方程,圆![]() 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
(2)求圆![]() 上的点到直线
上的点到直线![]() 的距离的最小值.
的距离的最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() (
(![]() ,且
,且![]() 为常数).
为常数).
(1)若函数![]() 的图象在
的图象在![]() 处的切线的斜率为
处的切线的斜率为![]() (
(![]() 为自然对数的底数),求
为自然对数的底数),求![]() 的值;
的值;
(2)若函数![]() 在区间
在区间![]() 上单调递增,求
上单调递增,求![]() 的取值范围;
的取值范围;
(3)已知![]() ,且
,且![]() .求证:
.求证:![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,
,![]() (
(![]() 为常数)对于任意的
为常数)对于任意的![]() 恒成立.
恒成立.
(1)若![]() ,求
,求![]() 的值;
的值;
(2)证明:数列![]() 是等差数列;
是等差数列;
(3)若![]() ,关于
,关于![]() 的不等式
的不等式![]() 有且仅有两个不同的整数解,求
有且仅有两个不同的整数解,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系![]() 中,椭圆
中,椭圆![]() 的方程为
的方程为![]() ,且直线
,且直线![]() 与以原点为圆心,椭圆
与以原点为圆心,椭圆![]() 短轴长为直径的圆相切.
短轴长为直径的圆相切.
(1)求![]() 的值;
的值;
(2)若椭圆![]() 左右顶点分别为
左右顶点分别为![]() ,过点
,过点![]() 作直线
作直线![]() 与椭圆交于
与椭圆交于![]() 两点,且
两点,且![]() 位于第一象限,
位于第一象限,![]() 在线段
在线段![]() 上.
上.
①若![]() 和
和![]() 的面积分别为
的面积分别为![]() ,问是否存在这样的直线
,问是否存在这样的直线![]() 使得
使得![]() ?请说明理由;
?请说明理由;
②直线![]() 与直线
与直线![]() 交于点
交于点![]() ,连结
,连结![]() ,记直线
,记直线![]() 的斜率分别为
的斜率分别为![]() ,求证:
,求证:![]() 为定值.
为定值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,某大型厂区有三个值班室![]() ,值班室
,值班室![]() 在值班室
在值班室![]() 的正北方向
的正北方向![]() 千米处,值班室
千米处,值班室![]() 在值班室
在值班室![]() 的正东方向
的正东方向![]() 千米处.
千米处.
(1)保安甲沿![]() 从值班室
从值班室![]() 出发行至点
出发行至点![]() 处,此时
处,此时![]() ,求
,求![]() 的距离;
的距离;
(2)保安甲沿![]() 从值班室
从值班室![]() 出发前往值班室
出发前往值班室![]() ,保安乙沿
,保安乙沿![]() 从值班室
从值班室![]() 出发前往值班室
出发前往值班室![]() ,甲乙同时出发,甲的速度为
,甲乙同时出发,甲的速度为![]() 千米/小时,乙的速度为
千米/小时,乙的速度为![]() 千米/小时,若甲乙两人通过对讲机联系,对讲机在厂区内的最大通话距离为
千米/小时,若甲乙两人通过对讲机联系,对讲机在厂区内的最大通话距离为![]() 千米(含
千米(含![]() 千米),试问有多长时间两人不能通话?
千米),试问有多长时间两人不能通话?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com