
科目: 来源: 题型:
【题目】某化工厂从今年一月起,若不改善生产环境,按生产现状,每月收入为80万元,同时将受到环保部门的处罚,第一个月罚4万元,以后每月增加2万元.如果从今年一月起投资500万元添加回收净化设备(改造设备时间不计),一方面可以改善环境,另一方面可以大大降低原料成本,据测算,添加回收净化设备并投产后的前4个月中的累计生产净收入g(n)是生产时间![]() 个月的二次函数
个月的二次函数![]() 是常数
是常数![]() ,且前3个月的累计生产净收入可达309万元,从第5个月开始,每个月的生产净收入都与第4个月相同,同时,该厂不但不受处罚,而且还将得到环保部门的一次性奖励120万元.
,且前3个月的累计生产净收入可达309万元,从第5个月开始,每个月的生产净收入都与第4个月相同,同时,该厂不但不受处罚,而且还将得到环保部门的一次性奖励120万元.
(1)求前6个月的累计生产净收入g(6)的值;
(2)问经过多少个月,投资开始见效,即投资改造后的纯收入多于不改造的纯收入.
查看答案和解析>>
科目: 来源: 题型:
【题目】二十四节气是中国古代的一种指导农事的补充历法,是我国劳动人民长期经验的积累成果和智慧的结晶,被誉为“中国的第五大发明”.由于二十四节气对古时候农事的进行起着非常重要的指导作用,所以劳动人民编写了很多记忆节气的歌谣:春雨惊春清谷天,夏满芒夏暑相连,秋处露秋寒霜降,冬雪雪冬小大寒.《易经》里对二十四节气的晷影长的记录中,冬至和夏至的晷影长是实测得到的,其他节气的晷影是按照等差数列的规律计算出来的,在下表中,冬至的晷影最长为130.0寸,夏至的晷影最短为14.8寸,那么《易经》中所记录的清明的晷影长应为( )

A.77.2寸B.72.4寸C.67.3寸D.62.8寸
查看答案和解析>>
科目: 来源: 题型:
【题目】若函数![]() 对定义城内的每一个值
对定义城内的每一个值![]() ,在其定义域内都存在唯一的
,在其定义域内都存在唯一的![]() ,使得
,使得![]() 成立,则称该函数为“
成立,则称该函数为“![]() 函数”.
函数”.
(1)判断函数![]() 是否为“
是否为“![]() 函数”,并说明理由;
函数”,并说明理由;
(2)若函数![]() 在定义域
在定义域![]() 上为“
上为“![]() 函数”,求
函数”,求![]() 的取值范围;
的取值范围;
(3)已知函数![]() 在定义域
在定义域![]() 上为“
上为“![]() 函数”.若存在实数
函数”.若存在实数![]() ,使得对任意的
,使得对任意的![]() ,不等式
,不等式![]() 都成立,求实数
都成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() ,
,![]() 是实数.
是实数.
(1)若函数![]() 是定义在
是定义在![]() 上的奇函数,求
上的奇函数,求![]() 的值,并求方程
的值,并求方程![]() 的解;
的解;
(2)若![]() 对任意的
对任意的![]() 恒成立,求
恒成立,求![]() 的取值范围;
的取值范围;
(3)若![]() ,方程
,方程![]() 有解,求实数
有解,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图:已知某公园的四处景观分别位于等腰梯形![]() 的四个顶点处,其中
的四个顶点处,其中![]() ,
,![]() 两地的距离为
两地的距离为![]() 千米,
千米,![]() ,
,![]() 两地的距离为
两地的距离为![]() 千米,
千米,![]() .现拟规划在
.现拟规划在![]() (不包括端点)路段上增加一个景观
(不包括端点)路段上增加一个景观![]() ,并建造观光路直接通往
,并建造观光路直接通往![]() 处,造价为每千米
处,造价为每千米![]() 万元,又重新装饰
万元,又重新装饰![]() 路段,造价为每千米
路段,造价为每千米![]() 万元.
万元.
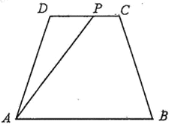
(1)若拟修建观光路![]() 路段长为
路段长为![]() 千米,求
千米,求![]() 路段的造价;
路段的造价;
(2)设![]() ,当
,当![]() 为何值时,
为何值时,![]() ,
,![]() 段的总造价最低.
段的总造价最低.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com