
科目: 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,已知曲线
中,已知曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数)。曲线
为参数)。曲线![]() 的参数方程为
的参数方程为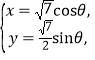 (
(![]() 为参数),在以坐标原点为极点,
为参数),在以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系.
轴正半轴为极轴建立极坐标系.
(1)求曲线![]() ,
,![]() 的极坐标方程;
的极坐标方程;
(2)在极坐标系中,射线![]() 与曲线
与曲线![]() 交于点
交于点![]() ,射线
,射线![]() 与曲线
与曲线![]() 交于点
交于点![]() ,求
,求![]() 的面积(其中
的面积(其中![]() 为坐标原点).
为坐标原点).
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() 的一个焦点与抛物线
的一个焦点与抛物线![]() 的焦点重合,且此抛物线的准线被椭圆
的焦点重合,且此抛物线的准线被椭圆![]() 截得的弦长为
截得的弦长为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)直线![]() 交椭圆
交椭圆![]() 于
于![]() 、
、![]() 两点,线段
两点,线段![]() 的中点为
的中点为![]() ,直线
,直线![]() 是线段
是线段![]() 的垂直平分线,试问直线
的垂直平分线,试问直线![]() 是否过定点?若是,请求出该定点的坐标;若不是,请说明理由.
是否过定点?若是,请求出该定点的坐标;若不是,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的左,右焦点分别为
的左,右焦点分别为![]() ,
,![]() ,点
,点![]() 为椭圆
为椭圆![]() 上任意一点,点
上任意一点,点![]() 关于原点
关于原点![]() 的对称点为点
的对称点为点![]() ,有
,有![]() ,且当
,且当![]() 的面积最大时为等边三角形.
的面积最大时为等边三角形.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)与圆![]() 相切的直线
相切的直线![]() :
:![]() 交椭圆
交椭圆![]() 于
于![]() ,
,![]() 两点,若椭圆上存在点
两点,若椭圆上存在点![]() 满足
满足![]() ,求四边形
,求四边形![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】为庆祝新中国成立七十周年,巴蜀中学将举行“歌唱祖国,喜迎国庆”歌咏比赛活动,《歌唱祖国》,《精忠报国》,《我和我的祖国》等一系列歌曲深受同学们的青睐,高二某班级就该班是否选择《精忠报国》作为本班参赛曲目进行投票表决,投票情况如下表.
小组 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
赞成人数 | 4 | 5 | 6 | 6 | 5 | 6 | 4 | 3 |
总人数 | 7 | 7 | 8 | 8 | 7 | 7 | 6 | 6 |
(1)若从第1小组和第8小组的同学中各随机选取2人进行调查,求所选取的4人中至少有2人赞成《精忠报国》作为本班参赛曲目的概率;
(2)若从第5小组和第7小组的同学中各随机选取2人进行调查,记选取的4人中不赞成《精忠报国》作为本班参赛曲目的人数为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() 的方程为
的方程为![]() ,椭圆
,椭圆![]() 的离心率正好是双曲线
的离心率正好是双曲线![]() 的离心率的倒数,椭圆
的离心率的倒数,椭圆![]() 的短轴长等于抛物线
的短轴长等于抛物线![]() 上一点
上一点![]() 到抛物线焦点
到抛物线焦点![]() 的距离.
的距离.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若直线![]() 与椭圆
与椭圆![]() 的两个交点为
的两个交点为![]() ,
,![]() 两点,已知圆
两点,已知圆![]() :
:![]() 与
与![]() 轴的交点分别为
轴的交点分别为![]() ,
,![]() (点
(点![]() 在
在![]() 轴的正半轴),且直线
轴的正半轴),且直线![]() 与圆
与圆![]() 相切,求
相切,求![]() 的面积与
的面积与![]() 的面积乘积的最大值.
的面积乘积的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】2014年12月19日,2014年中国数学奥林匹克竞赛(第30届全国中学生数学冬令营)在重庆市巴蜀中学举行.参加本届中国数学奥林匹克竞赛共有来自各省、市(自治区、直辖市)、香港地区、澳门地区,以及俄罗斯、新加坡等国的30余支代表队,共317名选手.竞赛为期2天,每天3道题,限时4个半小时完成.部分优胜者将参加为国际数学奥林匹克竞赛而组建的中国国家集训队.中国数学奥林匹克竞赛(全国中学生数学冬令营)是在全国高中数学联赛基础上进行的一次较高层次的数学竞赛,该项活动也是中国中学生级别最高、规模最大、最有影响的全国性数学竞赛.2020年第29届全国中学生生物学竞赛也将在重庆巴蜀中学举行.巴蜀中学校本选修课“数学建模”兴趣小组调查了2019年参加全国生物竞赛的200名学生(其中男生、女生各100人)的成绩,得到这200名学生成绩的中位数为78.这200名学生成绩均在50与110之间,且成绩在![]() 内的人数为30,这200名学生成绩的高于平均数的男生有62名,女生有38名.并根据调查结果画出如图所示的频率分布直方图.
内的人数为30,这200名学生成绩的高于平均数的男生有62名,女生有38名.并根据调查结果画出如图所示的频率分布直方图.
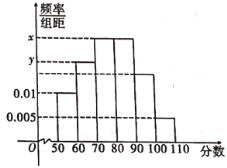
(1)求![]() ,
,![]() 的值;
的值;
(2)填写下表,能否有![]() 的把握认为学生成绩是否高于平均数与性别有关系?
的把握认为学生成绩是否高于平均数与性别有关系?
男生 | 女生 | 总计 | |
成绩不高于平均数 | |||
成绩高于平均数 | |||
总计 |
参考公式及数据: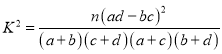 ,其中
,其中![]() .
.
| 0.05 | 0.01 | 0.005 | 0.001 |
| 3.841 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目: 来源: 题型:
【题目】已知,如图甲,正方形![]() 的边长为4,
的边长为4,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,以
的中点,以![]() 为棱将正方形
为棱将正方形![]() 折成如图乙所示,且
折成如图乙所示,且![]() ,点
,点![]() 在线段
在线段![]() 上且不与点
上且不与点![]() ,
,![]() 重合,直线
重合,直线![]() 与由
与由![]() ,
,![]() ,
,![]() 三点所确定的平面相交,交点为
三点所确定的平面相交,交点为![]() .
.
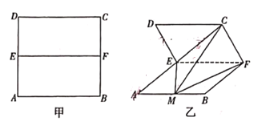
(1)若![]() ,试确定点
,试确定点![]() 的位置,并证明直线
的位置,并证明直线![]() 平面
平面![]() ;
;
(2)若![]() ,求点
,求点![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com