
科目: 来源: 题型:
【题目】如图,OH分别为锐角△ABC的外心垂心,AD⊥BC于D,G为AH的中点点K在线段GH上,且满足GK=HD,连结KO并延长交AB于点E.

(1) 证明:![]() ;
;
(2) 证明:![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和
的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
(2)已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,点
,点![]() 是曲线
是曲线![]() 与
与![]() 的交点,点
的交点,点![]() 是曲线
是曲线![]() 与
与![]() 的交点,
的交点,![]() 、
、![]() 均异于原点
均异于原点![]() ,且
,且![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】为利于分层教学,某学校根据学生的情况分成了![]() ,
,![]() ,
,![]() 三类,经过一段时间的学习后在三类学生中分别随机抽取了1个学生的5次考试成绩,其统计表如下:
三类,经过一段时间的学习后在三类学生中分别随机抽取了1个学生的5次考试成绩,其统计表如下:
![]() 类
类
第 | 1 | 2 | 3 | 4 | 5 |
分数 | 145 | 83 | 95 | 72 | 110 |
![]() ,
,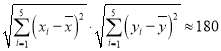 ;
;
![]() 类
类
第 | 1 | 2 | 3 | 4 | 5 |
分数 | 85 | 93 | 90 | 76 | 101 |
![]() ,
,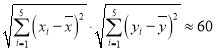 ;
;
![]() 类
类
第 | 1 | 2 | 3 | 4 | 5 |
分数 | 85 | 92 | 101 | 100 | 112 |
![]() ,
,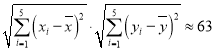 ;
;
(1)经计算已知![]() ,
,![]() 的相关系数分别为
的相关系数分别为![]() ,
,![]() ,请计算出
,请计算出![]() 学生的
学生的![]() 的相关系数,并通过数据的分析回答抽到的哪类学生学习成绩最稳定;(结果保留三位有效数字,
的相关系数,并通过数据的分析回答抽到的哪类学生学习成绩最稳定;(结果保留三位有效数字,![]() 越大认为成绩越稳定);
越大认为成绩越稳定);
(2)利用(1)中成绩最稳定的学生的样本数据,已知线性回归方程为![]() ,利用线性回归方程预测该生第九次的成绩.
,利用线性回归方程预测该生第九次的成绩.
参考公式:(1)样本![]() 的相关系数
的相关系数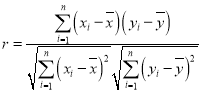 ;
;
(2)对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归方程
,其回归方程![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为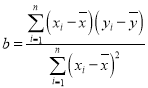 ,
,![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】由甲、乙、丙三个人组成的团队参加某项闯关游戏,第一关解密码锁,3个人依次进行,每人必须在1分钟内完成,否则派下一个人.3个人中只要有一人能解开密码锁,则该团队进入下一关,否则淘汰出局.根据以往100次的测试,分别获得甲、乙解开密码锁所需时间的频率分布直方图.
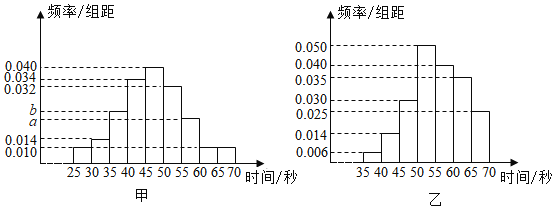
(1)若甲解开密码锁所需时间的中位数为47,求a、b的值,并分别求出甲、乙在1分钟内解开密码锁的频率;
(2)若以解开密码锁所需时间位于各区间的频率代替解开密码锁所需时间位于该区间的概率,并且丙在1分钟内解开密码锁的概率为0.5,各人是否解开密码锁相互独立.
①求该团队能进入下一关的概率;
②该团队以怎样的先后顺序派出人员,可使所需派出的人员数目X的数学期望达到最小,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com