【题目】已知函数.其中是自然对数的底数.

（1）求函数在点处的切线方程；

（2）若不等式对任意的恒成立，求实数的取值范围.

【题目】已知椭圆的左、右焦点分别为，离心率为，为椭圆上一动点（异于左右顶点），面积的最大值为．

（1）求椭圆的方程；

（2）若直线与椭圆相交于点两点，问轴上是否存在点，使得是以为直角顶点的等腰直角三角形？若存在，求点的坐标；若不存在，请说明理由．

（1）若此次问卷调查得分整体服从正态分布，用样本来估计总体，设，分别为这200人得分的平均值和标准差（同一组数据用该区间中点值作为代表），求，的值（，的值四舍五入取整数），并计算；

（2）在（1）的条件下，为感谢大家参与这次活动，市体育局还对参加问卷调查的幸运市民制定如下奖励方案：得分低于的可以获得1次抽奖机会，得分不低于的可获得2次抽奖机会，在一次抽奖中，抽中价值为15元的纪念品A的概率为，抽中价值为30元的纪念品B的概率为.现有市民张先生参加了此次问卷调查并成为幸运参与者，记Y为他参加活动获得纪念品的总价值，求Y的分布列和数学期望，并估算此次纪念品所需要的总金额.

（参考数据：；；.）

【题目】如图1，在等腰中，，，分别为，的中点，为的中点，在线段上，且。将沿折起，使点到的位置（如图2所示），且。

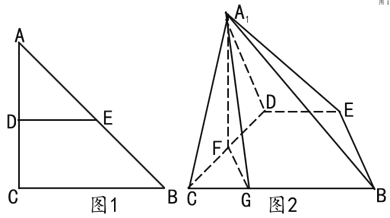
（1）证明：平面；

（2）求平面与平面所成锐二面角的余弦值

【题目】已知点是抛物线的准线上一点，F为抛物线的焦点，P为抛物线上的点，且，若双曲线C中心在原点，F是它的一个焦点，且过P点，当m取最小值时，双曲线C的离心率为______.

在直角坐标系中，曲线的参数方程为（为参数），以坐标原点为极点，轴正半轴为极轴建立极坐标系，直线的极坐标方程为.

（1）求直线与曲线公共点的极坐标；

（2）设过点的直线交曲线于，两点，且的中点为，求直线的斜率.

【题目】已知函数，其中为自然对数的底数.

（Ⅰ）当时，求证：时，；

（Ⅱ）当时，计论函数的极值点个数.

【题目】设、是椭圆的左、右顶点，为椭圆上异于、的一点．

（1）是椭圆的上顶点，且直线与直线垂直，求点到轴的距离；

（2）过点的直线（不过坐标原点）与椭圆交于、两点，且点在轴上方，点在轴下方，若，求直线的斜率．

【题目】如图，在四棱锥中，底面，底面是直角梯形，，，，点在上，且．

（1）点在上，，求证：平面；

（2）若直线与平面所成的角为，求二面角的余弦值．

满意率是指某种型号汽车的回访客户中，满意人数与总人数的比值．假设客户是否满意互相独立，且每种型号汽车客户对于此型号汽车满意的概率与表格中该型号汽车的满意率相等．

（1）从所有的回访客户中随机抽取1人，求这个客户满意的概率；

（2）从Ⅰ型号和Ⅴ型号汽车的所有客户中各随机抽取1人，设其中满意的人数为，求的分布列和期望．