【题目】设椭圆E:（a,b>0）过M（2，） ，N(,1)两点，O为坐标原点，

（1）求椭圆E的方程；

（2）是否存在圆心在原点的圆，使得该圆的任意一条切线与椭圆E恒有两个交点A,B,且？若存在，写出该圆的方程，若不存在说明理由．

【题目】某公司订购了一批树苗，为了检测这批树苗是否合格，从中随机抽测株树苗的高度，经数据处理得到如图1所示的频率分布直方图，其中最高的株树苗的高度的茎叶图如图2所示，以这株树苗的高度的频率估计整批树苗高度的概率.

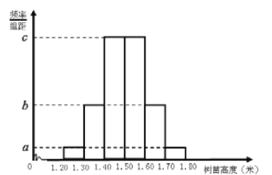
（1）求这批树苗的高度于米的概率，并求图中的值；

（2）若从这批树苗中随机选取株，记为高度在的树苗数量，求的分布列和数学期望；

（3）若变量满足且，则称变量满足近似于正态分布的概率分布，如果这批树苗的高度近似于正态分布的概率分布，则认为这批树苗是合格的，将顺利被签收，否则，公司将拒绝签收.试问：该批树苗是否被签收？

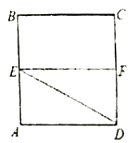
【题目】已知正方形，分别是的中点，将沿折起，如图所示，记二面角的大小为

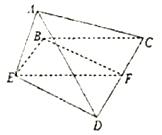
（1）证明：

（2）若为正三角形，试判断点在平面内的身影是否在直线上，证明你的结论，并求角的正弦值.

【题目】下列说法：①将一组数据中的每个数据都加上或减去同一个常数后，均值与方差都不变；②将某校参加摸底测试的1200名学生编号为1，2，3，…，1200，从中抽取一个容量为50的样本进行学习情况调查，按系统抽样的方法分为50组，如果第一组中抽出的学生编号为20，则第四组中抽取的学生编号为92；③线性回归方程必经过点；④在吸烟与患肺病这两个分类变量的计算中，从独立性检验知，有的把握认为吸烟与患肺病有关系时，我们说现有100人吸烟，那么其中有99人患肺病.其中错误的个数是( )

A.0B.1C.2D.3

【题目】某生鲜超市每天从蔬菜生产基地购进某种蔬菜，每天的进货量相同，进价6元/千克，售价9元/千克，当天未售出的蔬菜被生产基地以2元/千克的价格回收处理．该超市发现这种蔬菜每天都有剩余，为此整理了过往30天这种蔬菜的日需求量（单位：千克），得到如下统计数据：

以这30天记录的各日需求量的频率作为各日需求量的概率，假设各日需求量相互独立．

（1）求在未来的3天中，至多有1天的日需求量不超过190千克的概率；

（2）超市为了减少浪费，提升利润，决定调整每天的进货量（单位：千克），以销售这种蔬菜的日利润的期望值为决策依据，在与之中选其一，应选用哪个？

【题目】设圆的圆心为，直线过点且与轴不重合，交圆于，两点，过点作的平行线交于点.

（1）求的值；

（2）设点的轨迹为曲线，直线与曲线相交于，两点，与直线相交于点，试问在椭圆上是否存在一定点，使得，，成等差数列（其中，，分别指直线，，的斜率）.若存在，求出点的坐标；若不存在，请说明理由.

【题目】已知函数．

（1）讨论函数的单调性；

（2）若，，且存在不相等的实数，使得，求证且．

【题目】在平面直角坐标系中，以坐标原点为极点，轴的正半轴为极轴建立极坐标系，曲线的极坐标方程为，直线的极坐标方程为.

（1）求曲线与直线的直角坐标方程.

（2）直线与轴的交点为，与曲线的交点为，，求的值.

【题目】已知函数.

（1）关于的不等式的解集为，求的值；

（2）若函数的图象与轴围成图形的面积不小于50，求的取值范围.

【题目】如图所示，在长方体中，，，，过的截面的面积为，则的最小值为______．