
科目: 来源: 题型:
【题目】某单位鼓励员工参加健身运动,推广了一款手机软件,记录每人每天走路消耗的卡路里;软件的测评人员从员工中随机地选取了40人(男女各20人),记录他们某一天消耗的卡路里,并将数据整理如下:
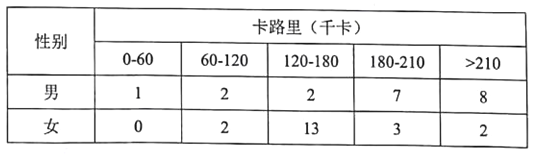
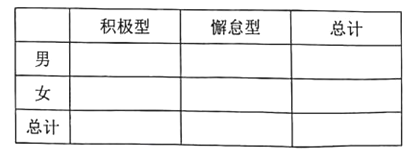
(1)已知某人一天的走路消耗卡路里超过180千卡被评测为“积极型”,否则为“懈怠型”,根据题中数据完成下面的![]() 列联表,并据此判断能否有99%以上把握认为“评定类型”与“性别”有关?
列联表,并据此判断能否有99%以上把握认为“评定类型”与“性别”有关?
(2)若测评人员以这40位员工每日走路所消耗的卡路里的频率分布来估计其所有员工每日走路消耗卡路里的频率分布,现在测评人员从所有员工中任选2人,其中每日走路消耗卡路里不超过120千卡的有![]() 人,超过210千卡的有
人,超过210千卡的有![]() 人,设
人,设![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
附: 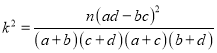 ,其中
,其中![]() .
.
参考数据:
| 0.10 | 0.05 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目: 来源: 题型:
【题目】设![]() 是两个非零平面向量,则有:
是两个非零平面向量,则有:
①若![]() ,则
,则![]()
②若![]() ,则
,则![]()
③若![]() ,则存在实数
,则存在实数![]() ,使得
,使得![]()
④若存在实数![]() ,使得
,使得![]() ,则
,则![]() 或
或![]() 四个命题中真命题的序号为 __________.(填写所有真命题的序号)
四个命题中真命题的序号为 __________.(填写所有真命题的序号)
【答案】①③④
【解析】逐一考查所给的结论:
①若![]() ,则
,则![]() ,据此有:
,据此有:![]() ,说法①正确;
,说法①正确;
②若![]() ,取
,取![]() ,则
,则![]() ,
,
而![]() ,说法②错误;
,说法②错误;
③若![]() ,则
,则![]() ,据此有:
,据此有:![]() ,
,
由平面向量数量积的定义有:![]() ,
,
则向量![]() 反向,故存在实数
反向,故存在实数![]() ,使得
,使得![]() ,说法③正确;
,说法③正确;
④若存在实数![]() ,使得
,使得![]() ,则向量
,则向量![]() 与向量
与向量![]() 共线,
共线,
此时![]() ,
,![]() ,
,
若题中所给的命题正确,则![]() ,
,
该结论明显成立.即说法④正确;
综上可得:真命题的序号为①③④.
点睛:处理两个向量的数量积有三种方法:利用定义;利用向量的坐标运算;利用数量积的几何意义.具体应用时可根据已知条件的特征来选择,同时要注意数量积运算律的应用.
【题型】填空题
【结束】
17
【题目】已知在![]() 中,
中,![]() ,且
,且![]() .
.
(1)求角![]() 的大小;
的大小;
(2)设数列![]() 满足
满足![]() ,前
,前![]() 项和为
项和为![]() ,若
,若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】若存在实常数k和b,使得函数![]() 对其公共定义域上的任意实数x都满足:
对其公共定义域上的任意实数x都满足:![]() 恒成立,则称此直线
恒成立,则称此直线![]() 的“隔离直线”,已知函数
的“隔离直线”,已知函数![]() (e为自然对数的底数),有下列命题:
(e为自然对数的底数),有下列命题:
①![]() 内单调递增;
内单调递增;
②![]() 之间存在“隔离直线”,且b的最小值为
之间存在“隔离直线”,且b的最小值为![]() ;
;
③![]() 之间存在“隔离直线”,且k的取值范围是
之间存在“隔离直线”,且k的取值范围是![]() ;
;
④![]() 之间存在唯一的“隔离直线”
之间存在唯一的“隔离直线”![]() .
.
其中真命题的序号为__________.(请填写正确命题的序号)
查看答案和解析>>
科目: 来源: 题型:
【题目】以平面直角坐标系![]() 的原点为极点,
的原点为极点,![]() 轴的正半轴为极轴,建立极坐标系,两种坐标系中取相同的长度单位,已知直线
轴的正半轴为极轴,建立极坐标系,两种坐标系中取相同的长度单位,已知直线![]() 的参数方程为
的参数方程为 ,曲线
,曲线![]() 的极坐标方程为
的极坐标方程为![]()
![]() 求直线
求直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
![]() 若把曲线
若把曲线![]() 上给点的横坐标伸长为原来的
上给点的横坐标伸长为原来的![]() 倍,纵坐标伸长为原来的
倍,纵坐标伸长为原来的![]() 倍,得到曲线
倍,得到曲线![]() ,设点
,设点![]() 是曲线
是曲线![]() 上的一个动点,求它到直线
上的一个动点,求它到直线![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() 的短轴长为
的短轴长为![]() ,离心率为
,离心率为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若动直线![]() 与椭圆
与椭圆![]() 有且仅有一个公共点,分别过
有且仅有一个公共点,分别过![]() 两点作
两点作![]() ,垂足分别为
,垂足分别为![]() ,且记
,且记![]() 为点
为点![]() 到直线
到直线![]() 的距离,
的距离, ![]() 为点
为点![]() 到直线
到直线![]() 的距离,
的距离,![]() 为点
为点![]() 到点
到点![]() 的距离,试探索
的距离,试探索![]() 是否存在最大值.若存在,求出最大值;若不存在,请说明理由.
是否存在最大值.若存在,求出最大值;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
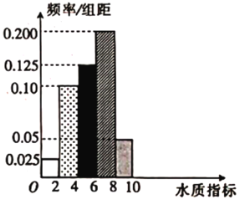
【题目】新《水污染防治法》已由中华人民共和国第十二届全国人民代表大会常务委员会第二十八次会议于2017年6月27日通过,自2018年1月1日起施行.2018年3月1日,某县某质检部门随机抽取了县域内100眼水井,检测其水质总体指标.
罗斯水质指数 | 02 | 24 | 46 | 68 | 810 |
水质状况 | 腐败污水 | 严重污染 | 污染 | 轻度污染 | 纯净 |
(1)求所抽取的100眼水井水质总体指标值的样本平均数![]() (同一组中的数据用该组区间的中点值作代表).
(同一组中的数据用该组区间的中点值作代表).
(2)①由直方图可以认为,100眼水井水质总体指标值![]() 服从正态分布
服从正态分布![]() ,利用该正态分布,求
,利用该正态分布,求![]() 落在(5.21,5.99)内的概率;
落在(5.21,5.99)内的概率;
②将频率视为概率,若某乡镇抽查5眼水井的水质,记这5眼水井水质总体指标值位于(6,10)内的井数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
附:①计算得所抽查的这100眼水井总体指标的标准差为![]() ;
;
②若![]() ,则
,则![]() ,
,![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() ).
).
(1)求曲线![]() 和直线
和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,且
两点,且![]() ,求以
,求以![]() 为直径的圆的方程.
为直径的圆的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com