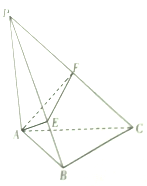
【题目】《九章算术》中，将四个面都为直角三角形的四面体称为鳖臑，如图，在鳖臑中，平面，，且，过点分别作于点，于点，连接，则三棱锥的体积的最大值为__________．

A. B. C. D.

【题目】在平面直角坐标系中，以为极点，轴的正半轴为极轴建立极坐标系，已知曲线，直线的参数方程为，（为参数）.直线与曲线交于两点.

（1）写出曲线的直角坐标方程和直线的普通方程.

（2）设，若成等比数列，求和的值.

【题目】在菱形中，，为线段的中点（如图1）．将沿折起到的位置，使得平面平面，为线段的中点（如图2）．

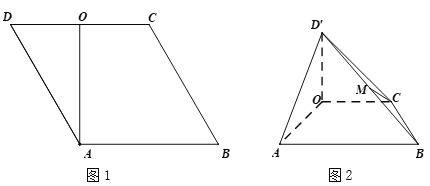
（Ⅰ）求证：；

（Ⅱ）求证：平面；

（Ⅲ）当四棱锥的体积为时，求的值．

高二

（1）若成绩不低于80分为“达标”，估计高一年级知识竞赛的达标率；

（2）在抽取的学生中，从成绩为的学生中随机选取2名学生，代表学校外出参加比赛，求这2名学生来自于同一年级的概率.

【题目】在直角坐标系中，曲线C的参数方程为为参数），以原点为极点，x轴的正半轴为极轴，建立极坐标系，曲线D的极坐标方程为.

（1）写出曲线C的极坐标方程以及曲线D的直角坐标方程；

（2）若过点（极坐标）且倾斜角为的直线l与曲线C交于M，N两点，弦MN的中点为P，求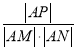的值．

【题目】已知抛物线C:的焦点为F，直线y=4与y轴的交点为P，与C的交点为Q，且.

(1)求抛物线C的方程；

(2)过F的直线l与C相交于A,B两点，若AB的垂直平分线与C相交于M,N两点，且A,M,B,N四点在同一个圆上，求直线l的方程.

已知函数， （为自然对数的底数）.

(Ⅰ)讨论的单调性；

(Ⅱ)当时，不等式恒成立，求实数的值.

若下面4个说法都是正确的：

①甲不在查资料，也不在写教案； ②乙不在打印材料，也不在查资料；

③丙不在批改作业，也不在打印材料； ④丁不在写教案，也不在查资料．

此外还可确定：如果甲不在打印材料，那么丙不在查资料．根据以上信息可以判断

【题目】在平面直角坐标系中，以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，已知曲线C的极坐标方程为＝（＞0），过点的直线的参数方程为（t为参数），直线与曲线C相交于A，B两点．

（Ⅰ）写出曲线C的直角坐标方程和直线的普通方程；

（Ⅱ）若，求的值．