【题目】已知函数.

(1)讨论的单调性;

(2)用表示中的最大值，若函数只有一个零点,求的取值范围.

【题目】如图，四棱锥P﹣ABCD的底面是梯形．BC∥AD，AB＝BC＝CD＝1，AD＝2，，

（Ⅰ）证明；AC⊥BP；

（Ⅱ）求直线AD与平面APC所成角的正弦值．

【题目】某校为了解高三男生的体能达标情况，抽调了120名男生进行立定跳远测试，根据统计数据得到如下的频率分布直方图.若立定跳远成绩落在区间的左侧，则认为该学生属“体能不达标的学生，其中分别为样本平均数和样本标准差，计算可得（同一组中的数据用该组区间的中点值作代表）.

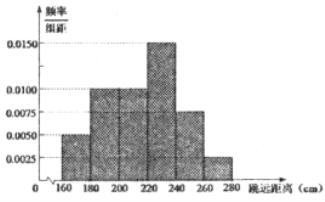
（1）若该校高三某男生的跳远距离为，试判断该男生是否属于“体能不达标”的学生？

（2）该校利用分层抽样的方法从样本区间中共抽出5人，再从中选出两人进行某体能训练，求选出的两人中恰有一人跳远距离在的概率.

A.B.C.D.

A. 甲的极差是29 B. 甲的中位数是24

C. 甲罚球命中率比乙高 D. 乙的众数是21

【题目】若数列对任意连续三项，均有，则称该数列为“跳跃数列”.

（1）判断下列两个数列是否是跳跃数列：

①等差数列：；

②等比数列：；

（2）若数列满足对任何正整数，均有.证明：数列是跳跃数列的充分必要条件是.

（3）跳跃数列满足对任意正整数均有，求首项的取值范围.

【题目】在平面直角坐标系中，，分别是椭圆的左、右焦点，直线与椭圆交于不同的两点、，且.

（1）求椭圆的方程；

（2）已知直线经过椭圆的右焦点，是椭圆上两点，四边形是菱形，求直线的方程；

（3）已知直线不经过椭圆的右焦点，直线，，的斜率依次成等差数列，求直线在轴上截距的取值范围.

【题目】疫情后，为了支持企业复工复产，某地政府决定向当地企业发放补助款，其中对纳税额在万元至万元（包括万元和万元）的小微企业做统一方案．方案要求同时具备下列两个条件：①补助款（万元）随企业原纳税额（万元）的增加而增加；②补助款不低于原纳税额（万元）的．经测算政府决定采用函数模型（其中为参数）作为补助款发放方案．

（1）判断使用参数是否满足条件，并说明理由；

（2）求同时满足条件①、②的参数的取值范围．

【题目】设集合，设集合是集合的非空子集，中的最大元素和最小元素之差称为集合的直径. 那么集合所有直径为的子集的元素个数之和为（ ）

A.B.C.D.

【题目】已知函数，.

（1）求证：存在唯一的实数，使得直线与曲线相切；

（2）若，，求证：.

（注：为自然对数的底数.）