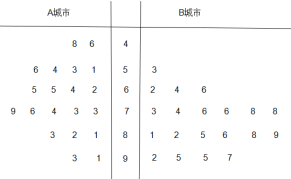
若评分不低于80分，则认为该用户对此授课方式“认可”，否则认为该用户对此授课方式“不认可”．以该样本中A，B城市的用户对此授课方式“认可”的频率分别作为A，B城市用户对此授课方式“认可”的概率．现从A城市和B城市的所有用户中分别随机抽取2个用户，用表示这4个用户中对此授课方式“认可”的用户个数，则__________；用表示从A城市随机抽取2个用户中对此授课方式“认可”的用户个数，则的数学期望为_________ ．

【题目】在平面直角坐标系中，以坐标原点O为极点，x轴正半轴为极轴，建立极坐标系，点，（）在曲线C：上，直线l过点且与垂直，垂足为P．

（Ⅰ）当时，求在直角坐标系下点P坐标和l的方程；

（Ⅱ）当M在C上运动且P在线段上时，求点P在极坐标系下的轨迹方程．

【题目】已知函数.

（1）若存在极值，求实数a的取值范围；

（2）设，设是定义在上的函数.

（ⅰ）证明：在上为单调递增函数(是的导函数)；

（ⅱ）讨论的零点个数.

【题目】在平面直角坐标系xOy中，过点的直线l与抛物线交于A，B两点，以AB为直径作圆，记为,与抛物线C的准线始终相切.

（1）求抛物线C的方程；

（2）过圆心M作x轴垂线与抛物线相交于点N，求的取值范围.

【题目】如图，真四棱柱的底面是菱形，，，，E，M，N分别是BC，，的中点.

（1）证明：面；

（2）求平面DMN与平面所成锐角的正切值.

【题目】已知棱长为2的正方体中，E为DC中点，F在线段上运动，则三棱锥的外接球的表面积最小值为（ ）

A.B.C.D.

【题目】已知直线的参数方程为（t为参数），以坐标原点为极点，正半轴为极轴，建立极坐标系，曲线的极坐标方程是．

（1）写出直线的极坐标方程与曲线的直角坐标方程；

（2）若点是曲线上的动点，求到直线距离的最小值，并求出此时点坐标．

（1）求实数a的取值范围；

（2）设两个极值点分别为x1，x2，x1＜x2，证明：f（x1）+f（x2）＜2﹣x12+x22.

【题目】已知椭圆C：的离心率为，与坐标轴分别交于A，B两点，且经过点Q（，1）．

（Ⅰ）求椭圆C的标准方程；

（Ⅱ）若P（m，n）为椭圆C外一动点，过点P作椭圆C的两条互相垂直的切线l1、l2，求动点P的轨迹方程，并求△ABP面积的最大值．

（I）求产生的手气红包的金额不小于9元的频率；

（Ⅱ）估计手气红包金额的平均数（同一组中的数据用该组区间的中点值作代表）；

（Ⅲ）在这50个红包组成的样本中，将频率视为概率．

（i）若红包金额在区间[21，25]内为最佳运气手，求抢得红包的某人恰好是最佳运气手的概率；

（ii）随机抽取手气红包金额在[1，5）∪[﹣21，25]内的两名幸运者，设其手气金额分别为m，n，求事件“|m﹣n|＞16”的概率．