
科目: 来源: 题型:
【题目】已知长轴长为![]() 的椭圆C:
的椭圆C:![]() 的左、右焦点分别为F1、F2,且以F1、F2为直径的圆与C恰有两个公共点.
的左、右焦点分别为F1、F2,且以F1、F2为直径的圆与C恰有两个公共点.
(1)求椭圆C的方程;
(2)若经过点F2的直线l与C交于M,N两点,且M,N关于原点O的对称点分别为P,Q,求四边形MNPQ面积的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】受突如其来的新冠疫情的影响,全国各地学校都推迟2020年的春季开学.某学校“停课不停学”,利用云课平台提供免费线上课程.该学校为了解学生对线上课程的满意程度,随机抽取了500名学生对该线上课程评分.其频率分布直方图如下:若根据频率分布直方图得到的评分低于80分的概率估计值为0.45.
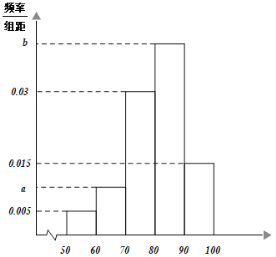
(1)(i)求直方图中的a,b值;
(ii)若评分的平均值和众数均不低于80分视为满意,判断该校学生对线上课程是否满意?并说明理由(同一组中的数据用该组区间的中点值为代表);
(2)若采用分层抽样的方法,从样本评分在[60,70)和[90,100]内的学生中共抽取5人进行测试来检验他们的网课学习效果,再从中选取2人进行跟踪分析,求这2人中至少一人评分在[60,70)内的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】在长方体ABCD﹣A1B1C1D1中,AA1=2AB=2AD=4,过AA1作平面α使BD⊥α,且平面α∩平面A1B1C1D1=l,M∈l.下面给出了四个命题:这四个命题中,真命题的个数为( )
①l∥AC;
②BM⊥AC;
③l和AD1所成的角为60°;
④线段BM长度的最小值为![]() .
.
A.1B.2C.3D.4
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,矩形ABCD中,![]() ,
,![]() ,E,F分别为AD,AB中点,M为线段BC上的一个动点,现将
,E,F分别为AD,AB中点,M为线段BC上的一个动点,现将![]() ,
,![]() ,分别沿EC,EF折起,使A,D重合于点P.设PM与平面BCEF所成角为
,分别沿EC,EF折起,使A,D重合于点P.设PM与平面BCEF所成角为![]() ,二面角
,二面角![]() 的平面角为
的平面角为![]() ,二面角
,二面角![]() 的平面角为
的平面角为![]() ,则( )
,则( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】在1,2,3,4,5,6这六个数字所组成的允许有重复数字的三位数中,各个数位上的数字之和为9的三位数共有( )
A.16个B.18个C.24个D.25个
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线C1的参数方程为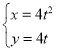 (其中t为参数).以坐标原点O为极点,x轴正半轴为极轴建立极坐标系并取相同的单位长度,曲线C2的极坐标方程为
(其中t为参数).以坐标原点O为极点,x轴正半轴为极轴建立极坐标系并取相同的单位长度,曲线C2的极坐标方程为![]() .
.
(1)把曲线C1的方程化为普通方程,C2的方程化为直角坐标方程;
(2)若曲线C1,C2相交于A,B两点,AB的中点为P,过点P做曲线C2的垂线交曲线C1于E,F两点,求|PE||PF|.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com