
科目: 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,左右顶点分别为
,左右顶点分别为![]() ,
,![]() ,右焦点为
,右焦点为![]() ,
,![]() 为椭圆上异于
为椭圆上异于![]() ,
,![]() 的动点,且
的动点,且![]() 面积的最大值为
面积的最大值为![]() .
.
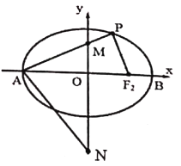
(1)求椭圆![]() 的方程;
的方程;
(2)设直线![]() 与
与![]() 轴交于
轴交于![]() 点,过点
点,过点![]() 作
作![]() 的平行线交
的平行线交![]() 轴与点
轴与点![]() ,试探究是否存在定点
,试探究是否存在定点![]() ,使得以
,使得以![]() 为直径的圆恒过定点
为直径的圆恒过定点![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】2019年春节前后,中国爆发新型冠状病毒(SARS-Cov-2)如图所示为1月24日至2月16日中国内地(除湖北以外的)感染新型冠状病毒新增人数的折线图,为了预测分析数据的变化规律,建立了![]() 与时间变量
与时间变量![]() 的不同时间段的两个线性回归模型.根据1月24日至2月3日的数据(时间变量
的不同时间段的两个线性回归模型.根据1月24日至2月3日的数据(时间变量![]() 的值依次为1,2,3,4,5,6,7,8,9,10,11)建立模型①:
的值依次为1,2,3,4,5,6,7,8,9,10,11)建立模型①:![]() ;根据2月4日至2月16日的数据(时间变量
;根据2月4日至2月16日的数据(时间变量![]() 的值依次为12,13,14,15,16,17,18,19,20,21,22,23,24)建立模型②:
的值依次为12,13,14,15,16,17,18,19,20,21,22,23,24)建立模型②:![]() .
.
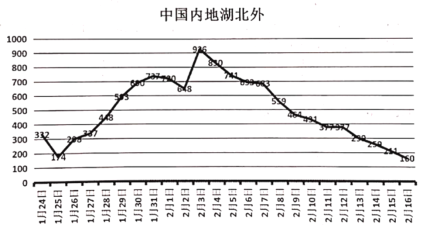
1月 24日 | 1月 25日 | 1月 26日 | 1月 27日 | 1月 28日 | 1月 29日 | 1月 30日 | 1月 31日 | 2月 1日 | 2月 2日 | 2月 3日 |
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
332 | 174 | 298 | 337 | 448 | 593 | 690 | 737 | 720 | 648 | 926 |
2月 4日 | 2月 5日 | 2月 6日 | 2月 7日 | 2月 8日 | 2月 9日 | 2月 10日 | 2月 11日 | 2月 12日 | 2月 13日 | 2月 14日 | 2月 15日 | 2月 16日 |
12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 |
830 | 741 | 693 | 683 | 559 | 464 | 431 | 377 | 377 | 299 | 259 | 211 | 160 |
(1)求出两个回归直线方程;(计算结果取整数)
(2)中国政府为了人民的生命安全,听取专家意见,了解了病毒信息,并迅速做出一系列的隔离防护措施,但新冠状病毒在世界范围内爆发时,某些欧美国家采取放任的态度,不治疗、不隔离、不检测,甚至不公布,请你用以上数据说明采取一系列措施的必要性,不采取措施的后果.
参考数据:![]() ,
,![]() ,
,![]() ,
,![]()
参考公式: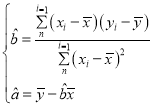 .
.
查看答案和解析>>
科目: 来源: 题型:
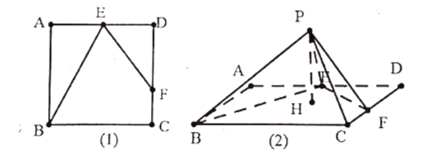
【题目】如图,边长为4的正方形![]() ,
,![]() 为
为![]() 中点,
中点,![]() 为
为![]() 边上一动点,现将
边上一动点,现将![]() ,
,![]() 分别沿
分别沿![]() ,
,![]() 折起,使得
折起,使得![]() ,
,![]() 重合为点
重合为点![]() ,形成四棱锥
,形成四棱锥![]() ,过点
,过点![]() 作
作![]() 平面
平面![]() 于
于![]() .①平面
.①平面![]() 平面
平面![]() ;②当
;②当![]() 为
为![]() 中点时,三棱锥
中点时,三棱锥![]() 的体积为
的体积为![]() ;③
;③![]() 为
为![]() 的垂心;④
的垂心;④![]() 长的取值范围为
长的取值范围为![]() .则以上判断正确的有______(填正确命题的序号).
.则以上判断正确的有______(填正确命题的序号).
查看答案和解析>>
科目: 来源: 题型:
【题目】中国有四大国粹:京剧、武术、中医和书法.某大学开设这四门课供学生选修,男生甲选其中三门课进行学习,已知他选修了京剧,则他选修书法的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】为进一步深化“平安校园”创建活动,加强校园安全教育宣传,某高中对该校学生进行了安全教育知识测试(满分100分),并从中随机抽取了200名学生的成绩,经过数据分析得到如图1所示的频数分布表,并绘制了得分在![]() 以及
以及![]() 的茎叶图,分别如图23所示.
的茎叶图,分别如图23所示.
成绩 |
|
|
|
|
|
|
|
频数 | 5 | 30 | 40 | 50 | 45 | 20 | 10 |
图1
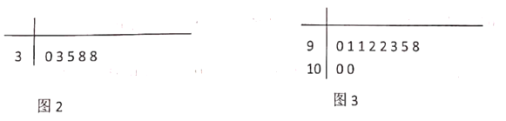
(1)求这200名同学得分的平均数;(同组数据用区间中点值作代表)
(2)如果变量![]() 满足
满足![]() 且
且![]() ,则称变量
,则称变量![]() “近似满足正态分布
“近似满足正态分布![]() 的概率分布”.经计算知样本方差为210,现在取
的概率分布”.经计算知样本方差为210,现在取![]() 和
和![]() 分别为样本平均数和方差,以样本估计总体,将频率视为概率,如果该校学生的得分“近似满足正态分布
分别为样本平均数和方差,以样本估计总体,将频率视为概率,如果该校学生的得分“近似满足正态分布![]() 的概率分布”,则认为该校的校园安全教育是成功的,否则视为不成功.试判断该校的安全教育是否成功,并说明理由.
的概率分布”,则认为该校的校园安全教育是成功的,否则视为不成功.试判断该校的安全教育是否成功,并说明理由.
(3)学校决定对90分及以上的同学进行奖励,为了体现趣味性,采用抽奖的方式进行,其中得分不低于94的同学有两次抽奖机会,低于94的同学只有一次抽奖机会,每次抽奖的奖金及对应的概率分别为:
奖金 | 50 | 100 |
概率 |
|
|
现在从不低于90同学中随机选一名同学,记其获奖金额为![]() ,以样本估计总体,将频率视为概率,求
,以样本估计总体,将频率视为概率,求![]() 的分布列和数学期望.
的分布列和数学期望.
(参考数据:![]() )
)
查看答案和解析>>
科目: 来源: 题型:
【题目】某水果批发商经销某种水果(以下简称![]() 水果),购入价为300元/袋,并以360元/袋的价格售出,若前8小时内所购进的
水果),购入价为300元/袋,并以360元/袋的价格售出,若前8小时内所购进的![]() 水果没有售完,则批发商将没售完的
水果没有售完,则批发商将没售完的![]() 水果以220元/袋的价格低价处理完毕(根据经验,2小时内完全能够把
水果以220元/袋的价格低价处理完毕(根据经验,2小时内完全能够把![]() 水果低价处理完,且当天不再购入).该水果批发商根据往年的销量,统计了100天
水果低价处理完,且当天不再购入).该水果批发商根据往年的销量,统计了100天![]() 水果在每天的前8小时内的销售量,制成如下频数分布条形图.
水果在每天的前8小时内的销售量,制成如下频数分布条形图.
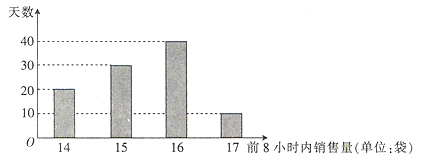
记![]() 表示
表示![]() 水果一天前8小时内的销售量,
水果一天前8小时内的销售量,![]() 表示水果批发商一天经营
表示水果批发商一天经营![]() 水果的利润,
水果的利润,![]() 表示水果批发商一天批发
表示水果批发商一天批发![]() 水果的袋数.
水果的袋数.
(1)若![]() ,求
,求![]() 与
与![]() 的函数解析式;
的函数解析式;
(2)假设这100天中水果批发商每天购入![]() 水果15袋或者16袋,分别计算该水果批发商这100天经营
水果15袋或者16袋,分别计算该水果批发商这100天经营![]() 水果的利润的平均数,以此作为决策依据,每天应购入
水果的利润的平均数,以此作为决策依据,每天应购入![]() 水果15袋还是16袋?
水果15袋还是16袋?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在正方体ABCD﹣A1B1C1D1中,M,N,P分别是C1D1,BC,A1D1的中点,有下列四个结论:
①AP与CM是异面直线;②AP,CM,DD1相交于一点;③MN∥BD1;
④MN∥平面BB1D1D.
其中所有正确结论的编号是( )

A.①④B.②④C.①④D.②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com