
科目: 来源: 题型:
【题目】2020年新年伊始,新型冠状病毒来势汹汹,疫情使得各地学生在寒假结束之后无法返校,教育部就此提出了线上教学和远程教学,停课不停学的要求也得到了家长们的赞同.各地学校开展各式各样的线上教学,某地学校为了加强学生爱国教育,拟开设国学课,为了了解学生喜欢国学是否与性别有关,该学校对100名学生进行了问卷调查,得到如下列联表:
喜欢国学 | 不喜欢国学 | 合计 | |
男生 | 20 | 50 | |
女生 | 10 | ||
合计 | 100 |
(1)请将上述列联表补充完整,并判断能否在犯错误的概率不超过0.001的前提下认为喜欢国学与性别有关系?
(2)针对问卷调查的100名学生,学校决定从喜欢国学的人中按分层抽样的方法随机抽取6人成立国学宣传组,并在这6人中任选2人作为宣传组的组长,设这两人中女生人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
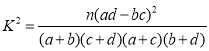 ,
,![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】给定下列四个命题,其中真命题是( )
A.垂直于同一直线的两条直线相互平行
B.若一个平面内的两条直线与另一个平面都平行,那么这两个平面相互平行
C.垂直于同一平面的两个平面相互平行
D.若两个平面垂直,那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直
查看答案和解析>>
科目: 来源: 题型:
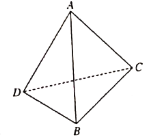
【题目】现有一副斜边长为10的直角三角板,将它们斜边![]() 重合,若将其中一个三角板沿斜边折起形成三棱锥
重合,若将其中一个三角板沿斜边折起形成三棱锥![]() ,如图所示,已知
,如图所示,已知![]() ,
,![]() ,则三棱锥
,则三棱锥![]() 的外接球的表面积为______;该三棱锥体积的最大值为_______.
的外接球的表面积为______;该三棱锥体积的最大值为_______.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知点![]() ,点A是直线
,点A是直线![]() 上的动点,过
上的动点,过![]() 作直线
作直线![]() ,
,![]() ,线段
,线段![]() 的垂直平分线与
的垂直平分线与![]() 交于点
交于点![]() .
.
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)若点![]() ,
,![]() 是直线
是直线![]() 上两个不同的点,且
上两个不同的点,且![]() 的内切圆方程为
的内切圆方程为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】 在新冠肺炎疫情的影响下,重庆市教委响应“停课不停教,停课不停学”的号召进行线上教学,某校高三年级的甲、乙两个班中,根据某次数学测试成绩各选出5名学生参加数学建模竞赛,已知这次测试他们取得的成绩的茎叶图如图所示,其中甲班5名学生成绩的平均分是83,乙班5名学生成绩的中位数是86.
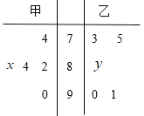
(1)求出![]() ,
,![]() 的值,且分别求甲、乙两个班中5名学生成绩的方差
的值,且分别求甲、乙两个班中5名学生成绩的方差![]() 、
、![]() ,并根据结果,你认为应该选派哪一个班的学生参加决赛,并说明你的理由.
,并根据结果,你认为应该选派哪一个班的学生参加决赛,并说明你的理由.
(2)从成绩在85分及以上的学生中随机抽取2名,用![]() 表示来自甲班的人数,求随机变量X的分布列与数学期望.
表示来自甲班的人数,求随机变量X的分布列与数学期望.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系xOy中,直线l的参数方程为![]() (t为参数),曲线C的参数方程为
(t为参数),曲线C的参数方程为![]() (θ为参数).
(θ为参数).
(1)当![]() 时,求直线l与曲线C的普通方程;
时,求直线l与曲线C的普通方程;
(2)若直线l与曲线C交于A,B两点,直线l倾斜角的范围为(0,![]() ],且P点的直角坐标为(0,2),求
],且P点的直角坐标为(0,2),求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com