
科目: 来源: 题型:
【题目】已知正△ABC边长为3,点M,N分别是AB,AC边上的点,AN=BM=1,如图1所示.将△AMN沿MN折起到△PMN的位置,使线段PC长为![]() ,连接PB,如图2所示.
,连接PB,如图2所示.
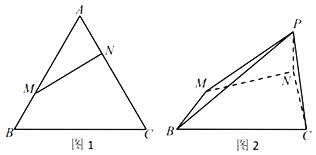
(Ⅰ)求证:平面PMN⊥平面BCNM;
(Ⅱ)若点D在线段BC上,且BD=2DC,求二面角M﹣PD﹣C的余弦值.
查看答案和解析>>
科目: 来源: 题型:
【题目】在棱长为1的正方体ABCD﹣A1B1C1D1中,点M,N分别是棱B1C1,C1D1的中点,过A,M,N三点作正方体的截面,将截面多边形向平面ADD1A1作投影,则投影图形的面积为_____.
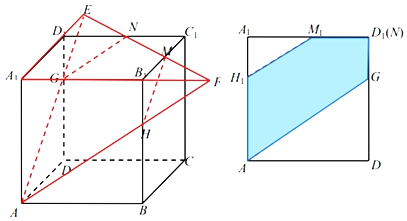
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,三棱锥S一ABC中,△ABC与△SBC都是边长为1的正三角形,二面角A﹣BC﹣S的大小为![]() ,若S,A,B,C四点都在球O的表面上,则球O的表面积为( )
,若S,A,B,C四点都在球O的表面上,则球O的表面积为( )
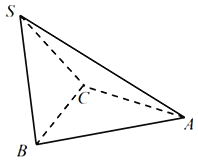
A.![]() πB.
πB.![]() πC.
πC.![]() πD.3π
πD.3π
查看答案和解析>>
科目: 来源: 题型:
【题目】设双曲线![]() 的左、右焦点分别为F1,F2,过点F2的直线分别交双曲线左、右两支于点P,Q,点M为线段PQ的中点,若P,Q,F1都在以M为圆心的圆上,且
的左、右焦点分别为F1,F2,过点F2的直线分别交双曲线左、右两支于点P,Q,点M为线段PQ的中点,若P,Q,F1都在以M为圆心的圆上,且![]() ,则双曲线C的离心率为( )
,则双曲线C的离心率为( )
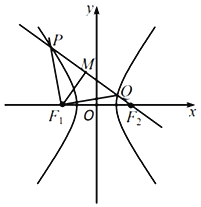
A.![]() B.2
B.2![]() C.
C.![]() D.2
D.2![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】在一个不透明的盒子中装有4个大小、形状、手感完全相同的小球,分别标有数字1,2,3,4.现每次有放回地从中任意取出一个小球,直到标有偶数的球都取到过就停止.小明用随机模拟的方法估计恰好在第4次停止摸球的概率,利用计算机软件产生随机数,每1组中有4个数字,分别表示每次摸球的结果,经随机模拟产生了以下21组随机数:由此可以估计恰好在第4次停止摸球的概率为( )
1314 1234 2333 1224 3322 1413 3124 4321 2341 2413 1224 2143 4312
2412 1413 4331 2234 4422 3241 4331 4234
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】如图是九江市2019年4月至2020年3月每月最低气温与最高气温(℃)的折线统计图:已知每月最低气温与最高气温的线性相关系数r=0.83,则下列结论错误的是( )
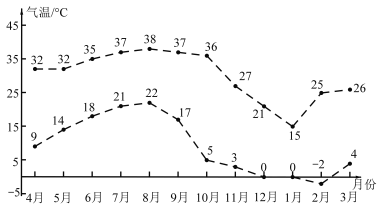
A.每月最低气温与最高气温有较强的线性相关性,且二者为线性正相关
B.月温差(月最高气温﹣月最低气温)的最大值出现在10月
C.9﹣12月的月温差相对于5﹣8月,波动性更大
D.每月最高气温与最低气温的平均值在前6个月逐月增加
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=|x|+|x﹣1|.
(1)若f(x)≥|m﹣1|恒成立,求实数m的最大值M;
(2)在(1)成立的条件下,正实数a,b满足a2+b2=M,证明:a+b≥2ab.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线![]() 上一点
上一点![]() 到其焦点下的距离为10.
到其焦点下的距离为10.
(1)求抛物线C的方程;
(2)设过焦点F的的直线![]() 与抛物线C交于
与抛物线C交于![]() 两点,且抛物线在
两点,且抛物线在![]() 两点处的切线分别交x轴于
两点处的切线分别交x轴于![]() 两点,求
两点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】绿水青山就是金山银山.某山村为做好水土保持,退耕还林,在本村的山坡上种植水果,并推出山村游等旅游项目.为预估今年7月份游客购买水果的情况,随机抽样统计了去年7月份100名游客的购买金额.分组如下:![]() ,
,![]() ,
,![]()
![]() ,得到如图所示的频率分布直方图:
,得到如图所示的频率分布直方图:
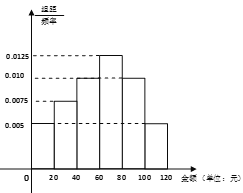
(1)请用抽样的数据估计今年7月份游客人均购买水果的金额(同一组中的数据用该组区间中点作代表).
(2)若把去年7月份购买水果不低于80元的游客,称为“水果达人”. 填写下面列联表,并根据列联表判断是否有95%的把握认为“水果达人”与性别有关系?
水果达人 | 非水果达人 | 合计 | |
男 | 10 | ||
女 | 30 | ||
合计 |
(3)为吸引顾客,商家特推出两种促销方案.方案一:每满80元可立减10元;方案二:金额超过80元可抽奖三次,每次中奖的概率为![]() ,且每次抽奖互不影响,中奖1次打9折,中奖2次打8折,中奖3次打7折.若每斤水果10元,你打算购买12斤水果,请从实际付款金额的数学期望的角度分析应该选择哪种优惠方案.
,且每次抽奖互不影响,中奖1次打9折,中奖2次打8折,中奖3次打7折.若每斤水果10元,你打算购买12斤水果,请从实际付款金额的数学期望的角度分析应该选择哪种优惠方案.
附:参考公式和数据:![]() ,
,![]() .临界值表:
.临界值表:
| 2.072 | 2.706 | 3.841 | 6.635 | 7.879 |
| 0.150 | 0.100 | 0.050 | 0.010 | 0.005 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com