
科目: 来源: 题型:
【题目】已知项数为![]() 的数列
的数列![]() 满足条件:①
满足条件:①![]() ;②
;②![]() ;若数列
;若数列![]() 满足
满足![]() ,则称
,则称![]() 为数列
为数列![]() 的“关联数列.
的“关联数列.
(1)数列1,5,9,13,17是否存在“关联数列”?若存在,写出其“关联数列”,若不存在,请说明理由;
(2)若数列![]() 存在“关联数列”
存在“关联数列”![]() ,证明:
,证明:![]() ;
;
(3)已知数列![]() 存在“关联数列”
存在“关联数列”![]() ,且
,且![]() ,
,![]() ,求数列
,求数列![]() 项数m的最小值与最大值.
项数m的最小值与最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】设双曲线![]() 的左顶点为D,且以点D为圆心的圆
的左顶点为D,且以点D为圆心的圆![]() 与双曲线C分别相交于点A、B,如图所示.
与双曲线C分别相交于点A、B,如图所示.
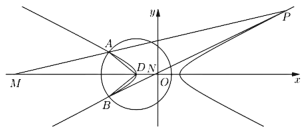
(1)求双曲线C的方程;
(2)求![]() 的最小值,并求出此时圆D的方程;
的最小值,并求出此时圆D的方程;
(3)设点P为双曲线C上异于点A、B的任意一点,且直线PA、PB分别与x轴相交于点M、N,求证:![]() 为定值(其中O为坐标原点).
为定值(其中O为坐标原点).
查看答案和解析>>
科目: 来源: 题型:
【题目】某工厂制作如图所示的一种标识,在半径为R的圆内做一个关于圆心对称的“H型”图形,“H”型图形由两竖一横三个等宽的矩形组成,两个竖直的矩形全等且它们的长边是横向矩形长边的![]() 倍,设O为圆心,
倍,设O为圆心,![]() ,“H”型图形的面积为S.
,“H”型图形的面积为S.
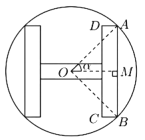
(1)将AB、AD用R、![]() 表示,并将S表示成
表示,并将S表示成![]() 的函数;
的函数;
(2)为了突出“H”型图形,设计时应使S尽可能大,则当![]() 为何值时,S最大?并求出S的最大值.
为何值时,S最大?并求出S的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知四棱锥![]() 的底面
的底面![]() 是矩形,
是矩形,![]() 底面
底面![]() ,且
,且![]() ,设E、F、G分别为PC、BC、CD的中点,H为EG的中点,如图.
,设E、F、G分别为PC、BC、CD的中点,H为EG的中点,如图.
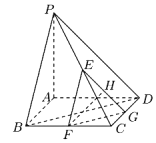
(1)求证:![]() 平面
平面![]() ;
;
(2)求直线FH与平面![]() 所成角的大小.
所成角的大小.
查看答案和解析>>
科目: 来源: 题型:
【题目】在等比数列![]() 中,已知
中,已知![]() 设数列
设数列![]() 的前n项和为
的前n项和为![]() ,且
,且![]()
(1)求数列![]() 通项公式;
通项公式;
(2)证明:数列![]() 是等差数列;
是等差数列;
(3)是否存在等差数列![]() ,使得对任意
,使得对任意![]() ,都有
,都有![]() ?若存在,求出所有符合题意的等差数列
?若存在,求出所有符合题意的等差数列![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知圆![]() 与椭圆
与椭圆![]() 相交于点M(0,1),N(0,-1),且椭圆的离心率为
相交于点M(0,1),N(0,-1),且椭圆的离心率为![]() .
.

(1)求![]() 的值和椭圆C的方程;
的值和椭圆C的方程;
(2)过点M的直线![]() 交圆O和椭圆C分别于A,B两点.
交圆O和椭圆C分别于A,B两点.
①若![]() ,求直线
,求直线![]() 的方程;
的方程;
②设直线NA的斜率为![]() ,直线NB的斜率为
,直线NB的斜率为![]() ,问:
,问:![]() 是否为定值? 如果是,求出定值;如果不是,说明理由.
是否为定值? 如果是,求出定值;如果不是,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】图①是一栋新农村别墅,它由上部屋顶和下部主体两部分组成.如图②,屋顶由四坡屋面构成,其中前后两坡屋面ABFE和CDEF是全等的等腰梯形,左右两坡屋面EAD和FBC是全等的三角形.点F在平面ABCD和BC上的射影分别为H,M.已知HM 5 m,BC 10 m,梯形ABFE的面积是△FBC面积的2.2倍.设∠FMH ![]()
![]() .
.
(1)求屋顶面积S关于![]() 的函数关系式;
的函数关系式;
(2)已知上部屋顶造价与屋顶面积成正比,比例系数为k(k为正的常数),下部主体造价与其 高度成正比,比例系数为16 k.现欲造一栋上、下总高度为6 m的别墅,试问:当![]() 为何值时,总造价最低?
为何值时,总造价最低?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com