
科目: 来源: 题型:
【题目】已知椭圆![]() 的离心率
的离心率![]() ,且椭圆过点
,且椭圆过点![]()
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设直线![]() 与
与![]() 交于
交于![]() 、
、![]() 两点,点
两点,点![]() 在椭圆
在椭圆![]() 上,
上,![]() 是坐标原点,若
是坐标原点,若![]() ,判定四边形
,判定四边形![]() 的面积是否为定值?若为定值,求出该定值;如果不是,请说明理由.
的面积是否为定值?若为定值,求出该定值;如果不是,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】在全面抗击新冠肺炎疫情这一特殊时期,我市教育局提出“停课不停学”的口号,鼓励学生线上学习.某校数学教师为了调查高三学生数学成绩与线上学习时间之间的相关关系,对高三年级随机选取45名学生进行跟踪问卷,其中每周线上学习数学时间不少于5小时的有19人,余下的人中,在检测考试中数学平均成绩不足120分的占![]() ,统计成绩后得到如下
,统计成绩后得到如下![]() 列联表:
列联表:
分数不少于120分 | 分数不足120分 | 合计 | |
线上学习时间不少于5小时 | 4 | 19 | |
线上学习时间不足5小时 | |||
合计 | 45 |
(1)请完成上面![]() 列联表;并判断是否有99%的把握认为“高三学生的数学成绩与学生线上学习时间有关”;
列联表;并判断是否有99%的把握认为“高三学生的数学成绩与学生线上学习时间有关”;
(2)在上述样本中从分数不少于120分的学生中,按照分层抽样的方法,抽到线上学习时间不少于5小时和线上学习时间不足5小时的学生共5名,若在这5名学生中随机抽取2人,求至少1人每周线上学习时间不足5小时的概率.
(下面的临界值表供参考)
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式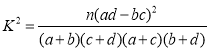 其中
其中![]() )
)
查看答案和解析>>
科目: 来源: 题型:
【题目】在四棱锥![]() 中,侧面PAD是等边三角形,且平面
中,侧面PAD是等边三角形,且平面![]() 平面ABCD,
平面ABCD,![]() ,
,![]() .
.
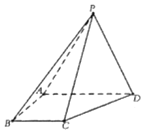
(1)AD上是否存在一点M,使得平面![]() 平面ABCD;若存在,请证明,若不存在,请说明理由;
平面ABCD;若存在,请证明,若不存在,请说明理由;
(2)若![]() 的面积为
的面积为![]() ,求四棱锥
,求四棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目: 来源: 题型:
【题目】《周髀算经》中给出了勾股定理的绝妙证明.如图是赵爽弦图及注文.弦图是一个以勾股形之弦为边的正方形,其面积称为弦实.图中包含四个全等的勾股形及一个小正方形,分别涂成朱色及黄色,其面积称为朱实、黄实.由2×勾×股+(股-勾)2=4×朱实+黄实=弦实,化简得勾2+股2=弦2.若图中勾股形的勾股比为![]() ,向弦图内随机抛掷100颗图钉(大小忽略不计),则落在黄色图形内的图钉颗数大约为( )(参考数据:
,向弦图内随机抛掷100颗图钉(大小忽略不计),则落在黄色图形内的图钉颗数大约为( )(参考数据:![]() ,
,![]() )
)
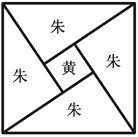
A.2B.4C.6D.8
查看答案和解析>>
科目: 来源: 题型:
【题目】![]() 是边长为
是边长为![]() 的等边三角形,E、F分别为AB、AC的中点,
的等边三角形,E、F分别为AB、AC的中点,![]() ,沿EF把
,沿EF把![]() 折起,使点A翻折到点P的位置,连接PB、PC,则四棱锥
折起,使点A翻折到点P的位置,连接PB、PC,则四棱锥![]() 的外接球的表面积的最小值为________,此时四棱锥
的外接球的表面积的最小值为________,此时四棱锥![]() 的体积为________.
的体积为________.
查看答案和解析>>
科目: 来源: 题型:
【题目】在直角坐标系中,曲线C的参数方程为![]() 为参数),以原点为极点,x轴的正半轴为极轴,建立极坐标系,曲线D的极坐标方程为
为参数),以原点为极点,x轴的正半轴为极轴,建立极坐标系,曲线D的极坐标方程为![]() .
.
(1)写出曲线C的极坐标方程以及曲线D的直角坐标方程;
(2)若过点![]() (极坐标)且倾斜角为
(极坐标)且倾斜角为![]() 的直线l与曲线C交于M,N两点,弦MN的中点为P,求
的直线l与曲线C交于M,N两点,弦MN的中点为P,求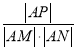 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某大型公司为了切实保障员工的健康安全,贯彻好卫生防疫工作的相关要求,决定在全公司范围内举行一次乙肝普查.为此需要抽验669人的血样进行化验,由于人数较多,检疫部门制定了下列两种可供选择的方案.
方案一:将每个人的血分别化验,这时需要验669次.
方案二:按![]() 个人一组进行随机分组,把从每组
个人一组进行随机分组,把从每组![]() 个人抽来的血混合在一起进行检验,如果每个人的血均为阴性,则验出的结果呈阴性,这
个人抽来的血混合在一起进行检验,如果每个人的血均为阴性,则验出的结果呈阴性,这![]() 个人的血就只需检验一次(这时认为每个人的血化验
个人的血就只需检验一次(这时认为每个人的血化验![]() 次);否则,若呈阳性,则需对这
次);否则,若呈阳性,则需对这![]() 个人的血样再分别进行一次化验,这时该组
个人的血样再分别进行一次化验,这时该组![]() 个人的血总共需要化验
个人的血总共需要化验![]() 次.
次.
假设此次普查中每个人的血样化验呈阳性的概率为![]() ,且这些人之间的试验反应相互独立.
,且这些人之间的试验反应相互独立.
(1)设方案二中,某组![]() 个人中每个人的血化验次数为
个人中每个人的血化验次数为![]() ,求
,求![]() 的分布列.
的分布列.
(2)设![]() ,试比较方案二中,
,试比较方案二中,![]() 分别取2,3,4时,各需化验的平均总次数;并指出在这三种分组情况下,相比方案一,化验次数最多可以平均减少多少次?(最后结果四舍五入保留整数)
分别取2,3,4时,各需化验的平均总次数;并指出在这三种分组情况下,相比方案一,化验次数最多可以平均减少多少次?(最后结果四舍五入保留整数)
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线![]() (
(![]() )上的两个动点
)上的两个动点![]() 和
和![]() ,焦点为F.线段AB的中点为
,焦点为F.线段AB的中点为![]() ,且A,B两点到抛物线的焦点F的距离之和为8.
,且A,B两点到抛物线的焦点F的距离之和为8.
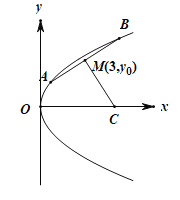
(1)求抛物线的标准方程;
(2)若线段AB的垂直平分线与x轴交于点C,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com