
科目: 来源: 题型:
【题目】已知椭圆![]() 的左顶点为A,O为坐标原点,
的左顶点为A,O为坐标原点,![]() ,C的离心率为
,C的离心率为![]() .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)已知不经过点A的直线![]() 交椭圆C于M,N两点,线段MN的中点为B,若
交椭圆C于M,N两点,线段MN的中点为B,若![]() ,求证:直线l过定点.
,求证:直线l过定点.
查看答案和解析>>
科目: 来源: 题型:
【题目】某病毒研究所为了研究温度对某种病毒的影响,在温度t(℃)逐渐升高时,连续测20次病毒的活性指标值y,实验数据处理后得到下面的散点图,将第1~14组数据定为A组,第15~20组数据定为B组.
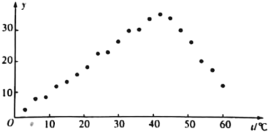
(Ⅰ)某研究员准备直接根据全部20组数据用线性回归模型拟合y与t的关系,你认为是否合理?请从统计学的角度简要说明理由.
(Ⅱ)若根据A组数据得到回归模型![]() ,根据B组数据得到回归模型
,根据B组数据得到回归模型![]() ,以活性指标值大于5为标准,估计这种病毒适宜生存的温度范围(结果精确到0.1).
,以活性指标值大于5为标准,估计这种病毒适宜生存的温度范围(结果精确到0.1).
(Ⅲ)根据实验数据计算可得:A组中活性指标值的平均数![]() ,方差
,方差![]()
![]() ;B组中活性指标值的平均数
;B组中活性指标值的平均数![]() ,方差
,方差![]() .请根据以上数据计算全部20组活性指标值的平均数
.请根据以上数据计算全部20组活性指标值的平均数![]() 和方差
和方差![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,三棱锥![]() 中,
中,![]() ,
,![]() 是正三角形,且平面
是正三角形,且平面![]() 平面ABC,
平面ABC,![]() ,E,G分别为AB,BC的中点.
,E,G分别为AB,BC的中点.

(Ⅰ)证明:![]() 平面ABD;
平面ABD;
(Ⅱ)若F是线段DE的中点,求AC与平面FGC所成角的正弦值.
查看答案和解析>>
科目: 来源: 题型:
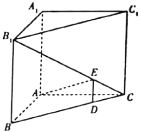
【题目】如图,在直三棱柱![]() 中,
中,![]() ,
,![]() ,点D,E分别是线段BC,
,点D,E分别是线段BC,![]() 上的动点(不含端点),且
上的动点(不含端点),且![]() .则下列说法正确的是( )
.则下列说法正确的是( )
A.![]() 平面
平面![]()
B.该三棱柱的外接球的表面积为![]()
C.异面直线![]() 与
与![]() 所成角的正切值为
所成角的正切值为![]()
D.二面角![]() 的余弦值为
的余弦值为![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】小张上班从家到公司开车有两条线路,所需时间(分钟)随交通堵塞状况有所变化,其概率分布如下表所示:
所需时间(分钟) | 30 | 40 | 50 | 60 |
线路一 | 0.5 | 0.2 | 0.2 | 0.1 |
线路二 | 0.3 | 0.5 | 0.1 | 0.1 |
则下列说法正确的是( )
A.任选一条线路,“所需时间小于50分钟”与“所需时间为60分钟”是对立事件
B.从所需的平均时间看,线路一比线路二更节省时间
C.如果要求在45分钟以内从家赶到公司,小张应该走线路一
D.若小张上、下班走不同线路,则所需时间之和大于100分钟的概率为0.04
查看答案和解析>>
科目: 来源: 题型:
【题目】已知动圆![]() 过点
过点![]() 且与直线
且与直线![]() 相切.
相切.
(1)求圆心![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过![]() 的直线与
的直线与![]() 交于
交于![]() ,
,![]() 两点,分别过
两点,分别过![]() ,
,![]() 做
做![]() 的垂线,垂足为
的垂线,垂足为![]() ,
,![]() ,线段
,线段![]() 的中点为
的中点为![]() .
.
①求证:![]() ;
;
②记四边形![]() ,
,![]() 的面积分别为
的面积分别为![]() ,
,![]() ,若
,若![]() ,求
,求![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】近年来,政府相关部门引导乡村发展旅游的同时,鼓励农户建设温室大棚种植高品质农作物.为了解某农作物的大棚种植面积对种植管理成本的影响,甲,乙两同学一起收集6家农户的数据,进行回归分折,得到两个回归摸型:模型①:![]() ,模型②:
,模型②: ![]() ,对以上两个回归方程进行残差分析,得到下表:
,对以上两个回归方程进行残差分析,得到下表:
种植面积 | 2 | 3 | 4 | 5 | 7 | 9 | |
每亩种植管理成本 | 25 | 24 | 21 | 22 | 16 | 14 | |
模型① | 估计值 | 25.27 | 23.62 | 21.97 | 17.02 | 13.72 | |
残差 | -0.27 | 0.38 | -0.97 | -1.02 | 0.28 | ||
模型② |
| 26.84 | 20.17 | 18.83 | 17.31 | 16.46 | |
| -1.84 | 0.83 | 3.17 | -1.31 | -2.46 | ||
(1)将以上表格补充完整,并根据残差平方和判断哪个模型拟合效果更好;
(2)视残差![]() 的绝对值超过1.5的数据视为异常数据,针对(1)中拟合效果较好的模型,剔除异常数据后,重新求回归方程.
的绝对值超过1.5的数据视为异常数据,针对(1)中拟合效果较好的模型,剔除异常数据后,重新求回归方程.
附: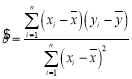 ,
,![]() ;
;![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】在正方体![]() 中,点
中,点![]() 是线段
是线段![]() 上的动点,以下结论:
上的动点,以下结论:
①![]() 平面
平面![]() ;
;
②![]() ;
;
③三棱锥![]() ,体积不变;
,体积不变;
④![]() 为
为![]() 中点时,直线
中点时,直线![]() 与平面
与平面![]() 所成角最大.
所成角最大.
其中正确的序号为( )
A.①④B.②④C.①②③D.①②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com