
科目: 来源: 题型:
【题目】以平面直角坐标系的原点O为极点,x轴非负半轴为极轴,并在两种坐标系中取相同的长度单位,建立极坐标系.曲线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 的参数方程为
的参数方程为![]() ,(
,(![]() 为参数).
为参数).
(1)求曲线![]() 的直角坐标方程及
的直角坐标方程及![]() 的普通方程;
的普通方程;
(2)已知点PQ为曲线![]() 与曲线
与曲线![]() 的交点,W为参数方程
的交点,W为参数方程![]() (
(![]() 为参数)曲线
为参数)曲线![]() 上一点,求点W到直线
上一点,求点W到直线![]() 的距离d的最大值.
的距离d的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆C:![]() (
(![]() )的左右焦点分别为
)的左右焦点分别为![]()
![]() ,点
,点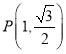 满足:
满足:![]() ,且
,且![]() .
.
(1)求椭圆C的标准方程;
(2)过点![]() 的直线l与C交于
的直线l与C交于![]() ,
,![]() 不同的两点,且
不同的两点,且![]() ,问在x轴上是否存在定点N,使得直线
,问在x轴上是否存在定点N,使得直线![]() ,
,![]() 与y轴围成的三角形始终为底边在y轴上的等腰三角形.若存在,求定点N的坐标;若不存在,请说明理由.
与y轴围成的三角形始终为底边在y轴上的等腰三角形.若存在,求定点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】某市为广泛开展垃圾分类的宣传教育和倡导工作,使市民树立垃圾分类的环保意识,学会垃圾分类的知识,特举办了“垃圾分类知识竞赛".据统计,在为期1个月的活动中,共有两万人次参与网络答题.市文明实践中心随机抽取100名参与该活动的市民,以他们单次答题得分作为样本进行分析,由此得到如图所示的频率分布直方图:

(1)求图中a的值及参与该活动的市民单次挑战得分的平均成绩![]() (同一组中数据用该组区间中点值作代表);
(同一组中数据用该组区间中点值作代表);
(2)若垃圾分类答题挑战赛得分落在区间![]() 之外,则可获得一等奖奖励,其中
之外,则可获得一等奖奖励,其中![]() ,s分别为样本平均数和样本标准差,计算可得
,s分别为样本平均数和样本标准差,计算可得![]() ,若某人的答题得分为96分,试判断此人是否获得一等奖;
,若某人的答题得分为96分,试判断此人是否获得一等奖;
(3)为扩大本次“垃圾分类知识竞赛”活动的影响力,市文明实践中心再次组织市民组队参场有奖知识竞赛,竞赛共分五轮进行,已知“光速队”与“超能队”五轮的成绩如下表:
成绩 | 第一轮 | 第二轮 | 第三轮 | 第四轮 | 第五轮 |
“光速队” | 93 | 98 | 94 | 95 | 90 |
“超能队” | 93 | 96 | 97 | 94 | 90 |
①分别求“光速队”与“超能队”五轮成绩的平均数和方差;
②以上述数据为依据,你认为"光速队”与“超能队”的现场有奖知识竞赛成绩谁更稳定?
查看答案和解析>>
科目: 来源: 题型:
【题目】新冠疫情发生后,酒精使用量大增,某生产企业调整设备,全力生产![]() 与
与![]() 两种不同浓度的酒精,按照计划可知在一个月内,酒精日产量
两种不同浓度的酒精,按照计划可知在一个月内,酒精日产量![]() (单位:吨)与时间n(
(单位:吨)与时间n(![]() 且
且![]() )成等差数列,且
)成等差数列,且![]() ,
,![]() .又知
.又知![]() 酒精日产量所占比重
酒精日产量所占比重![]() 与时间n成等比数列,
与时间n成等比数列,![]() 酒精日产量所占比重与时间n的关系如下表(
酒精日产量所占比重与时间n的关系如下表(![]() ):
):
|
|
|
| …… |
时间n | 1 | 2 | 3 | …… |
(1)求![]() ,
,![]() 的通项公式;
的通项公式;
(2)若![]() ,求前n天
,求前n天![]() (单位:吨,
(单位:吨,![]() 且
且![]() ).
).
查看答案和解析>>
科目: 来源: 题型:
【题目】假设你有一笔资金,现有三种投资方案,这三种方案的回报如下:
方案一:每天回报40元;
方案二:第一天回报10元,以后每天比前一天多回报10元;
方案三:第一天回报0.4元,以后每天的回报比前一天翻一番.
现打算投资10天,三种投资方案的总收益分别为![]() ,
,![]() ,
,![]() ,则( )
,则( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】袋中装有黑球和白球共7个,从中任取2个球都是白球的概率为![]() ,现有甲,乙二人从袋中轮流摸取1球,甲先取,乙后取,然后甲再取,……,取后不放回,直到两人中有一人取到白球即终止,每个球在每一次被取出的机会是等可能的.
,现有甲,乙二人从袋中轮流摸取1球,甲先取,乙后取,然后甲再取,……,取后不放回,直到两人中有一人取到白球即终止,每个球在每一次被取出的机会是等可能的.
(Ⅰ)求袋中原有白球的个数:
(Ⅱ)求取球次数![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com