
科目: 来源: 题型:
【题目】设椭圆![]() 的离心率与双曲线
的离心率与双曲线![]() 的离心率互为倒数,且内切于圆
的离心率互为倒数,且内切于圆![]() .
.
(1)求椭圆M的方程;
(2)已知R![]() 是椭圆M上的一动点,从原点O引圆R:
是椭圆M上的一动点,从原点O引圆R:![]() 的两条切线,分别交椭圆M于P、Q两点,直线OP与直线OQ的斜率分别为
的两条切线,分别交椭圆M于P、Q两点,直线OP与直线OQ的斜率分别为![]() ,试探究
,试探究![]() 是否为定值并证明你所探究出的结论.
是否为定值并证明你所探究出的结论.
查看答案和解析>>
科目: 来源: 题型:
【题目】若定义在R上的函数![]() ,其图像是连续不断的,且存在常数
,其图像是连续不断的,且存在常数![]() 使得
使得![]() 对任意实数x都成立,则称
对任意实数x都成立,则称![]() 是一个“k~特征函数”.则下列结论中正确命题序号为____________.
是一个“k~特征函数”.则下列结论中正确命题序号为____________.
①![]() 是一个“k~特征函数”;②
是一个“k~特征函数”;②![]() 不是“k~特征函数”;
不是“k~特征函数”;
③![]() 是常数函数中唯一的“k~特征函数”;④“
是常数函数中唯一的“k~特征函数”;④“![]() ~特征函数”至少有一个零点;
~特征函数”至少有一个零点;
查看答案和解析>>
科目: 来源: 题型:
【题目】2019年2月13日《烟台市全民阅读促进条例》全文发布,旨在保障全民阅读权利,培养全民阅读习惯,提高全民阅读能力,推动文明城市和文化强市建设.某高校为了解条例发布以来全校学生的阅读情况,随机调查了200名学生每周阅读时间![]() (单位:小时)并绘制如图所示的频率分布直方图.
(单位:小时)并绘制如图所示的频率分布直方图.

(1)求这200名学生每周阅读时间的样本平均数![]() 和中位数
和中位数![]() (
(![]() 的值精确到0.01);
的值精确到0.01);
(2)为查找影响学生阅读时间的因素,学校团委决定从每周阅读时间为![]() ,
,![]() 的学生中抽取9名参加座谈会.
的学生中抽取9名参加座谈会.
(i)你认为9个名额应该怎么分配?并说明理由;
(ii)座谈中发现9名学生中理工类专业的较多.请根据200名学生的调研数据,填写下面的列联表,并判断是否有![]() 的把握认为学生阅读时间不足(每周阅读时间不足8.5小时)与“是否理工类专业”有关?
的把握认为学生阅读时间不足(每周阅读时间不足8.5小时)与“是否理工类专业”有关?
阅读时间不足8.5小时 | 阅读时间超过8.5小时 | |
理工类专业 | 40 | 60 |
非理工类专业 |
附:![]() (
(![]() ).
).
临界值表:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| <> | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目: 来源: 题型:
【题目】某同学用“随机模拟方法”计算曲线![]() 与直线
与直线![]() 所围成的曲边三角形的面积时,用计算机分别产生了10个在区间[1,e]上的均匀随机数xi和10个在区间[0,1]上的均匀随机数
所围成的曲边三角形的面积时,用计算机分别产生了10个在区间[1,e]上的均匀随机数xi和10个在区间[0,1]上的均匀随机数![]()
![]() ,其数据如下表的前两行.
,其数据如下表的前两行.
x | 2.50 | 1.01 | 1.90 | 1.22 | 2.52 | 2.17 | 1.89 | 1.96 | 1.36 | 2.22 |
y | 0.84 | 0.25 | 0.98 | 0.15 | 0.01 | 0.60 | 0.59 | 0.88 | 0.84 | 0.10 |
lnx | 0.90 | 0.01 | 0.64 | 0.20 | 0.92 | 0.77 | 0.64 | 0.67 | 0.31 | 0.80 |
由此可得这个曲边三角形面积的一个近似值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() 的左顶点为
的左顶点为![]() ,右焦点为
,右焦点为![]() ,
,![]() ,
,![]() 为椭圆
为椭圆![]() 上两点,圆
上两点,圆![]() .
.
(1)若![]() 轴,且满足直线
轴,且满足直线![]() 与圆
与圆![]() 相切,求圆
相切,求圆![]() 的方程;
的方程;
(2)若圆![]() 的半径为2,点
的半径为2,点![]() ,
,![]() 满足
满足![]() ,求直线
,求直线![]() 被圆
被圆![]() 截得弦长的最大值.
截得弦长的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某媒体为调查喜爱娱乐节目![]() 是否与观众性别有关,随机抽取了30名男性和30名女性观众,抽查结果用等高条形图表示如图:
是否与观众性别有关,随机抽取了30名男性和30名女性观众,抽查结果用等高条形图表示如图:
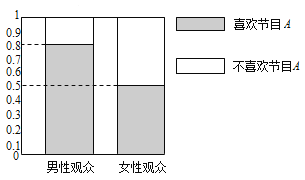
(1)根据该等高条形图,完成下列![]() 列联表,并用独立性检验的方法分析,能否在犯错误的概率不超过0.05的前提下认为喜欢娱乐节目
列联表,并用独立性检验的方法分析,能否在犯错误的概率不超过0.05的前提下认为喜欢娱乐节目![]() 与观众性别有关?
与观众性别有关?

(2)从性观众中按喜欢节目![]() 与否,用分层抽样的方法抽取5名做进一步调查.从这5名中任选2名,求恰有1名喜欢节目
与否,用分层抽样的方法抽取5名做进一步调查.从这5名中任选2名,求恰有1名喜欢节目![]() 和1名不喜欢节目
和1名不喜欢节目![]() 的概率.
的概率.
附:
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
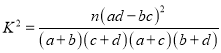 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com