
科目: 来源: 题型:
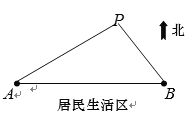
【题目】如图所示,![]() 、
、![]() 是两个垃圾中转站,
是两个垃圾中转站,![]() 在
在![]() 的正东方向
的正东方向![]() 千米处,
千米处,![]() 的南面为居民生活区.为了妥善处理生活垃圾,政府决定在
的南面为居民生活区.为了妥善处理生活垃圾,政府决定在![]() 的北面建一个垃圾发电厂
的北面建一个垃圾发电厂![]() .垃圾发电厂
.垃圾发电厂![]() 的选址拟满足以下两个要求(
的选址拟满足以下两个要求(![]() 、
、![]() 、
、![]() 可看成三个点):①垃圾发电厂到两个垃圾中转站的距离与它们每天集中的生活垃圾量成反比,比例系数相同;②垃圾发电厂应尽量远离居民区(这里参考的指标是点
可看成三个点):①垃圾发电厂到两个垃圾中转站的距离与它们每天集中的生活垃圾量成反比,比例系数相同;②垃圾发电厂应尽量远离居民区(这里参考的指标是点![]() 到直线
到直线![]() 的距离要尽可能大).现估测得
的距离要尽可能大).现估测得![]() 、
、![]() 两个中转站每天集中的生活垃圾量分别约为
两个中转站每天集中的生活垃圾量分别约为![]() 吨和
吨和![]() 吨.设
吨.设![]() .
.
(1)求![]() (用
(用![]() 的表达式表示);
的表达式表示);
(2)垃圾发电厂该如何选址才能同时满足上述要求?
查看答案和解析>>
科目: 来源: 题型:
【题目】已知二次函数![]() 的图象的顶点坐标为
的图象的顶点坐标为![]() ,且过坐标原点O,数列
,且过坐标原点O,数列![]() 的前n项和为
的前n项和为![]() ,点
,点![]() (
(![]() )在二次函数
)在二次函数![]() 的图象上.
的图象上.
(1)求数列![]() 的表达式;
的表达式;
(2)设![]() (
(![]() ),数列
),数列![]() 的前n项和为
的前n项和为![]() ,若
,若![]() 对
对![]() 恒成立,求实数m的取值范围;
恒成立,求实数m的取值范围;
(3)在数列![]() 中是否存在这样的一些项,
中是否存在这样的一些项,![]() ,
,![]() ,
,![]() ,…
,…![]() ,…(
,…(![]() ),这些项能够依次构成以
),这些项能够依次构成以![]() 为首项,q(
为首项,q(![]() ,
,![]() )为公比的等比数列
)为公比的等比数列![]() ?若存在,写出
?若存在,写出![]() 关于k的表达式;若不存在,说明理由.
关于k的表达式;若不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系![]() 中,动点
中,动点![]() 到定点
到定点![]() 的距离与它到直线
的距离与它到直线![]() 的距离相等.
的距离相等.
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)设动直线![]() 与曲线
与曲线![]() 相切于点
相切于点![]() ,与直线
,与直线![]() 相交于点
相交于点![]() .
.
证明:以![]() 为直径的圆恒过
为直径的圆恒过![]() 轴上某定点.
轴上某定点.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在三棱锥![]() 中,
中,![]() 底面
底面![]() ,
,![]() ,
,![]() .D,E分别为
.D,E分别为![]() ,
,![]() 的中点,过
的中点,过![]() 的平面与
的平面与![]() ,
,![]() 相交于点M,N(M与P,B不重合,N与P,C不重合).
相交于点M,N(M与P,B不重合,N与P,C不重合).
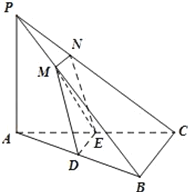
(1)求证:![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的大小;
所成角的大小;
(3)若直线![]() 与直线
与直线![]() 所成角的余弦值
所成角的余弦值![]() 时,求
时,求![]() 的长.
的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】某地区有800名学员参加交通法规考试,考试成绩的频率分布直方图如图所示,其中成绩分组区间是:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,规定90分及以上为合格:
,规定90分及以上为合格:
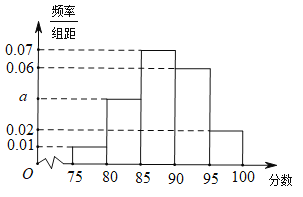
(1)求图中a的值;
(2)根据频率分布直方图估计该地区学员交通法规考试合格的概率;
(3)若三个人参加交通法规考试,估计这三个人至少有两人合格的概率.
查看答案和解析>>
科目: 来源: 题型:
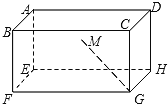
【题目】如图所示,在长方体![]() 中,AD=2,AB=AE=1,M为矩形AEHD内的一点,如果∠MGF=∠MGH,MG和平面EFG所成角的正切值为
中,AD=2,AB=AE=1,M为矩形AEHD内的一点,如果∠MGF=∠MGH,MG和平面EFG所成角的正切值为![]() 那么点M到平面EFGH的距离是_____.
那么点M到平面EFGH的距离是_____.
查看答案和解析>>
科目: 来源: 题型:
【题目】对于无穷数列![]() ,
,![]() ,若
,若![]() -
-![]()
![]() …,则称
…,则称![]() 是
是![]() 的“收缩数列”.其中,
的“收缩数列”.其中,![]() ,
,![]() 分别表示
分别表示![]() 中的最大数和最小数.已知
中的最大数和最小数.已知![]() 为无穷数列,其前
为无穷数列,其前![]() 项和为
项和为![]() ,数列
,数列![]() 是
是![]() 的“收缩数列”.
的“收缩数列”.
(1)若![]() ,求
,求![]() 的前
的前![]() 项和;
项和;
(2)证明:![]() 的“收缩数列”仍是
的“收缩数列”仍是![]() ;
;
(3)若![]() ,求所有满足该条件的
,求所有满足该条件的![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() 的定义域为
的定义域为![]() ,设
,设![]() ,
,![]() .
.
(Ⅰ)试确定t的取值范围,使得函数![]() 在
在![]() 上为单调函数;
上为单调函数;
(Ⅱ)求证:![]() ;
;
(Ⅲ)求证:对于任意的![]() ,总存在
,总存在![]() ,满足
,满足![]() ,又若方程
,又若方程![]() 在
在![]() 上有唯一解,请确定t的取值范围.
上有唯一解,请确定t的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com