
科目: 来源: 题型:
【题目】已知函数f(x)![]() .
.
(1)求函数y=f(x)的单调区间;
(2)若曲线y=f(x)与直线y=b(b∈R)有3个交点,求实数b的取值范围;
(3)过点P(﹣1,0)可作几条直线与曲线y=f(x)相切?请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知a,b是不相等的两个正数,在a,b之间插入两组实数:x1,x2,…,xn和y1,y2,…,yn,(n∈N*,且n≥2),使得a,x1,x2,…,xn,b成等差数列,a,y1,y2,…,yn,b成等比数列,给出下列四个式子:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中一定成立的是( )
.其中一定成立的是( )
A.①②③B.①②④C.①③④D.②③④
查看答案和解析>>
科目: 来源: 题型:
【题目】对于自然数数组![]() ,如下定义该数组的极差:三个数的最大值与最小值的差.如果
,如下定义该数组的极差:三个数的最大值与最小值的差.如果![]() 的极差
的极差![]() ,可实施如下操作
,可实施如下操作![]() :若
:若![]() 中最大的数唯一,则把最大数减2,其余两个数各增加1;若
中最大的数唯一,则把最大数减2,其余两个数各增加1;若![]() 中最大的数有两个,则把最大数各减1,第三个数加2,此为一次操作,操作结果记为
中最大的数有两个,则把最大数各减1,第三个数加2,此为一次操作,操作结果记为![]() ,其级差为
,其级差为![]() .若
.若![]() ,则继续对
,则继续对![]() 实施操作
实施操作![]() ,…,实施
,…,实施![]() 次操作后的结果记为
次操作后的结果记为![]() ,其极差记为
,其极差记为![]() .例如:
.例如:![]() ,
,![]() .
.
(1)若![]() ,求
,求![]() 和
和![]() 的值;
的值;
(2)已知![]() 的极差为
的极差为![]() 且
且![]() ,若
,若![]() 时,恒有
时,恒有![]() ,求
,求![]() 的所有可能取值;
的所有可能取值;
(3)若![]() 是以4为公比的正整数等比数列中的任意三项,求证:存在
是以4为公比的正整数等比数列中的任意三项,求证:存在![]() 满足
满足![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,焦距为
,焦距为![]() .斜率为k的直线l与椭圆M有两个不同的交点A,B.
.斜率为k的直线l与椭圆M有两个不同的交点A,B.
(Ⅰ)求椭圆M的方程;
(Ⅱ)若![]() ,求
,求![]() 的最大值;
的最大值;
(Ⅲ)设![]() ,直线PA与椭圆M的另一个交点为C,直线PB与椭圆M的另一个交点为D.若C,D和点
,直线PA与椭圆M的另一个交点为C,直线PB与椭圆M的另一个交点为D.若C,D和点![]() 共线,求k.
共线,求k.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,正三角形ABE与菱形ABCD所在的平面互相垂直,![]() ,
,![]() ,M是AB的中点.
,M是AB的中点.
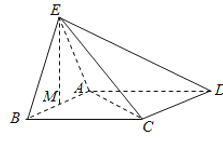
(1)求证:![]() ;
;
(2)求二面角![]() 的余弦值;
的余弦值;
(3)在线段EC上是否存在点P,使得直线AP与平面ABE所成的角为![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】春节期间,受烟花爆竹集中燃放影响,我国多数城市空气中![]() 浓度快速上升,特别是在大气扩散条件不利的情况下,空气质量在短时间内会迅速恶化
浓度快速上升,特别是在大气扩散条件不利的情况下,空气质量在短时间内会迅速恶化![]() 年除夕18时和初一2时,国家环保部门对8个城市空气中
年除夕18时和初一2时,国家环保部门对8个城市空气中![]() 浓度监测的数据如表
浓度监测的数据如表![]() 单位:微克
单位:微克![]() 立方米
立方米![]() .
.
除夕18时 | 初一2时 | |
北京 | 75 | 647 |
天津 | 66 | 400 |
石家庄 | 89 | 375 |
廊坊 | 102 | 399 |
太原 | 46 | 115 |
上海 | 16 | 17 |
南京 | 35 | 44 |
杭州 | 131 | 39 |
![]() Ⅰ
Ⅰ![]() 求这8个城市除夕18时空气中
求这8个城市除夕18时空气中![]() 浓度的平均值;
浓度的平均值;
![]() Ⅱ
Ⅱ![]() 环保部门发现:除夕18时到初一2时空气中
环保部门发现:除夕18时到初一2时空气中![]() 浓度上升不超过100的城市都是“禁止燃放烟花爆竹“的城市,浓度上升超过100的城市都未禁止燃放烟花爆竹
浓度上升不超过100的城市都是“禁止燃放烟花爆竹“的城市,浓度上升超过100的城市都未禁止燃放烟花爆竹![]() 从以上8个城市中随机选取3个城市组织专家进行调研,记选到“禁止燃放烟花爆竹”的城市个数为X,求随机变量y的分布列和数学期望;
从以上8个城市中随机选取3个城市组织专家进行调研,记选到“禁止燃放烟花爆竹”的城市个数为X,求随机变量y的分布列和数学期望;
![]() Ⅲ
Ⅲ![]() 记2017年除夕18时和初一2时以上8个城市空气中
记2017年除夕18时和初一2时以上8个城市空气中![]() 浓度的方差分别为
浓度的方差分别为![]() 和
和![]() ,比较
,比较![]() 和
和![]() 的大小关系
的大小关系![]() 只需写出结果
只需写出结果![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】若函数![]() 对其定义域内的任意
对其定义域内的任意![]() ,
,![]() ,当
,当![]() 时总有
时总有![]() ,则称
,则称![]() 为紧密函数,例如函数
为紧密函数,例如函数![]() 是紧密函数,下列命题:
是紧密函数,下列命题:
![]() 紧密函数必是单调函数;
紧密函数必是单调函数;![]() 函数
函数![]() 在
在![]() 时是紧密函数;
时是紧密函数;
![]() 函数
函数![]() 是紧密函数;
是紧密函数;
![]() 若函数
若函数![]() 为定义域内的紧密函数,
为定义域内的紧密函数,![]() ,则
,则![]() ;
;
![]() 若函数
若函数![]() 是紧密函数且在定义域内存在导数,则其导函数
是紧密函数且在定义域内存在导数,则其导函数![]() 在定义域内的值一定不为零.
在定义域内的值一定不为零.
其中的真命题是______.
查看答案和解析>>
科目: 来源: 题型:
【题目】在直角坐标系![]() 中,对于点
中,对于点![]() ,定义变换
,定义变换![]() :将点
:将点![]() 变换为点
变换为点![]() ,使得
,使得![]() 其中
其中![]() .这样变换
.这样变换![]() 就将坐标系
就将坐标系![]() 内的曲线变换为坐标系
内的曲线变换为坐标系![]() 内的曲线.则四个函数
内的曲线.则四个函数![]() ,
,![]() ,
,![]() ,
,![]() 在坐标系
在坐标系![]() 内的图象,变换为坐标系
内的图象,变换为坐标系![]() 内的四条曲线(如图)依次是
内的四条曲线(如图)依次是

A. ②,③,①,④B. ③,②,④,①C. ②,③,④,①D. ③,②,①,④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com