
科目: 来源: 题型:
【题目】设集合![]() 、
、![]() 均为实数集
均为实数集![]() 的子集,记:
的子集,记:![]() ;
;
(1)已知![]() ,
,![]() ,试用列举法表示
,试用列举法表示![]() ;
;
(2)设![]() ,当
,当![]() ,且
,且![]() 时,曲线
时,曲线![]() 的焦距为
的焦距为![]() ,如果
,如果![]() ,
,![]() ,设
,设![]() 中的所有元素之和为
中的所有元素之和为![]() ,对于满足
,对于满足![]() ,且
,且![]() 的任意正整数
的任意正整数![]() 、
、![]() 、
、![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的最大值;
的最大值;
(3)若整数集合![]() ,则称
,则称![]() 为“自生集”,若任意一个正整数均为整数集合
为“自生集”,若任意一个正整数均为整数集合![]() 的某个非空有限子集中所有元素的和,则称
的某个非空有限子集中所有元素的和,则称![]() 为“
为“![]() 的基底集”,问:是否存在一个整数集合既是自生集又是
的基底集”,问:是否存在一个整数集合既是自生集又是![]() 的基底集?请说明理由.
的基底集?请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】设![]() 为两个随机事件,给出以下命题:(1)若
为两个随机事件,给出以下命题:(1)若![]() 为互斥事件,且
为互斥事件,且![]() ,
,![]() ,则
,则![]() ;(2)若
;(2)若![]() ,
,![]() ,
,![]() ,则
,则![]() 为相互独立事件;(3)若
为相互独立事件;(3)若![]() ,
,![]() ,
,![]() ,则
,则![]() 为相互独立事件;(4)若
为相互独立事件;(4)若![]() ,
,![]() ,
,![]() ,则
,则![]() 为相互独立事件;(5)若
为相互独立事件;(5)若![]() ,
,![]() ,
,![]() ,则
,则![]() 为相互独立事件;其中正确命题的个数为( )
为相互独立事件;其中正确命题的个数为( )
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目: 来源: 题型:
【题目】对于定义域为R的函数![]() ,若函数
,若函数![]() 是奇函数,则称
是奇函数,则称![]() 为正弦奇函数.已知
为正弦奇函数.已知![]() 是单调递增的正弦奇函数,其值域为R,
是单调递增的正弦奇函数,其值域为R,![]() .
.
(1)已知![]() 是正弦奇函数,证明:“
是正弦奇函数,证明:“![]() 为方程
为方程![]() 的解”的充要条件是“
的解”的充要条件是“![]() 为方程
为方程![]() 的解”;
的解”;
(2)若![]()
![]() ,求
,求![]() 的值;
的值;
(3)证明:![]() 是奇函数.
是奇函数.
查看答案和解析>>
科目: 来源: 题型:
【题目】若数列![]() 对任意的
对任意的![]() ,都有
,都有![]()
![]() ,且
,且![]() ,则称数列
,则称数列![]() 为“k级创新数列”.
为“k级创新数列”.
(1)已知数列![]() 满足
满足![]() 且
且![]() ,试判断数列
,试判断数列![]() 是否为“2级创新数列”,并说明理由;
是否为“2级创新数列”,并说明理由;
(2)已知正数数列![]() 为“k级创新数列”且
为“k级创新数列”且![]() ,若
,若![]() ,求数列
,求数列![]() 的前n项积
的前n项积![]() ;
;
(3)设![]() ,
,![]() 是方程
是方程![]() 的两个实根
的两个实根![]() ,令
,令![]() ,在(2)的条件下,记数列
,在(2)的条件下,记数列![]() 的通项
的通项![]() ,求证:
,求证:![]()
![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】某地计划在一处海滩建造一个养殖场.
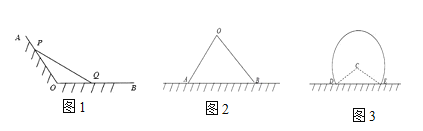
(1)如图1,射线OA,OB为海岸线,![]() ,现用长度为1千米的围网PQ依托海岸线围成一个
,现用长度为1千米的围网PQ依托海岸线围成一个![]() 的养殖场,问如何选取点P,Q,才能使养殖场
的养殖场,问如何选取点P,Q,才能使养殖场![]() 的面积最大,并求其最大面积.
的面积最大,并求其最大面积.
(2)如图2,直线l为海岸线,现用长度为1千米的围网依托海岸线围成一个养殖场.方案一:围成三角形OAB(点A,B在直线l上),使三角形OAB面积最大,设其为![]() ;方案二:围成弓形CDE(点D,E在直线l上,C是优弧所在圆的圆心且
;方案二:围成弓形CDE(点D,E在直线l上,C是优弧所在圆的圆心且![]() ),其面积为
),其面积为![]() ;试求出
;试求出![]() 的最大值和
的最大值和![]() (均精确到0.01平方千米),并指出哪一种设计方案更好.
(均精确到0.01平方千米),并指出哪一种设计方案更好.
查看答案和解析>>
科目: 来源: 题型:
【题目】某公司新研发了一款手机应用APP,投入市场三个月后,公司对部分用户做了调研:抽取了400位使用者,每人填写一份综合评分表(满分为100分).现从400份评分表中,随机抽取40份(其中男、女使用者的评分表各20份)作为样本,经统计得到如下的茎叶图:
女性使用者评分 | 男性使用者评分 | |
7 | 6 | 7 8 9 9 |
1 2 5 | 7 | 0 2 2 3 4 5 6 6 7 8 9 |
0 3 3 3 4 4 5 6 6 8 | 8 | 2 4 4 9 |
0 0 1 2 2 2 | 9 | 2 |
记该样本的中位数为![]() ,按评分情况将使用者对该APP的态度分为三种类型:评分不小于
,按评分情况将使用者对该APP的态度分为三种类型:评分不小于![]() 的称为“满意型”,评分不大于
的称为“满意型”,评分不大于![]() 的称为“不满意型”,其余的都称为“须改进型”.
的称为“不满意型”,其余的都称为“须改进型”.
(1)求![]() 的值,并估计这400名使用者中“须改进型”使用者的个数;
的值,并估计这400名使用者中“须改进型”使用者的个数;
(2)为了改进服务,公司对“不满意型”使用者进行了回访,根据回访意见改进后,再从“不满意型”使用者中随机抽取3人进行第二次调查,记这3人中的女性使用者人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目: 来源: 题型:
【题目】西湖小学为了丰富学生的课余生活开设课后少年宫活动,其中面向二年级的学生共开设了三门课外活动课:七巧板、健美操、剪纸.203班有包括奔奔、果果在内的5位同学报名参加了少年宫活动,每位同学只能挑选一门课外活动课,已知每门课都有人选,则奔奔和果果选择了同一个课外活动课的选课方法种数为( )
A.18B.36C.72D.144
查看答案和解析>>
科目: 来源: 题型:
【题目】如图是国家统计局给出的2014年至2018年我国城乡就业人员数量的统计图表,结合这张图表,以下说法错误的是( )
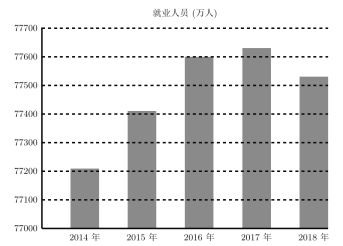
A.2017年就业人员数量是最多的
B.2017年至2018年就业人员数量呈递减状态
C.2016年至2017年就业人员数量与前两年比较,增加速度减缓
D.2018年就业人员数量比2014年就业人员数量增长超过400万人
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com