
科目: 来源: 题型:
【题目】已知椭圆C:![]() (
(![]() )的两焦点与短轴两端点围成面积为12的正方形.
)的两焦点与短轴两端点围成面积为12的正方形.
(1)求椭圆C的标准方程;
(2)我们称圆心在椭圆上运动,半径为![]() 的圆是椭圆的“卫星圆”.过原点O作椭圆C的“卫星圆”的两条切线,分别交椭圆C于A、B两点,若直线
的圆是椭圆的“卫星圆”.过原点O作椭圆C的“卫星圆”的两条切线,分别交椭圆C于A、B两点,若直线![]() 、
、![]() 的斜率为
的斜率为![]() 、
、![]() ,当
,当![]() 时,求此时“卫星圆”的个数.
时,求此时“卫星圆”的个数.
查看答案和解析>>
科目: 来源: 题型:
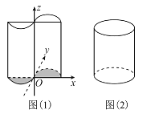
【题目】我国古代数学家祖暅提出原理:“幂势既同,则积不容异”.其中“幂”是截面积,“势”是几何体的高.原理的意思是:夹在两个平行平面间的两个几何体,被任一平行于这两个平行平面的平面所截,若所截的两个截面的面积恒相等,则这两个几何体的体积相等.如图(1),函数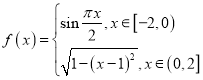 的图象与x轴围成一个封闭区域A(阴影部分),将区域A(阴影部分)沿z轴的正方向上移6个单位,得到一几何体.现有一个与之等高的底面为椭圆的柱体如图(2)所示,其底面积与区域A(阴影部分)的面积相等,则此柱体的体积为______.
的图象与x轴围成一个封闭区域A(阴影部分),将区域A(阴影部分)沿z轴的正方向上移6个单位,得到一几何体.现有一个与之等高的底面为椭圆的柱体如图(2)所示,其底面积与区域A(阴影部分)的面积相等,则此柱体的体积为______.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,将![]() 方格纸中每个小方格染三种颜色之一,使得每种颜色的小方格的个数相等.若相邻两个小方格的颜色不同,称他们的公共边为“分割边”,则分割边条数的最小值为( )
方格纸中每个小方格染三种颜色之一,使得每种颜色的小方格的个数相等.若相邻两个小方格的颜色不同,称他们的公共边为“分割边”,则分割边条数的最小值为( )

A.33B.56C.64D.78
查看答案和解析>>
科目: 来源: 题型:
【题目】已知![]() 为坐标原点,椭圆
为坐标原点,椭圆![]() :
:![]() 的焦距为
的焦距为![]() ,直线
,直线![]() 截圆
截圆![]() :
:![]() 与椭圆
与椭圆![]() 所得的弦长之比为
所得的弦长之比为![]() ,椭圆
,椭圆![]() 与
与![]() 轴正半轴的交点分别为
轴正半轴的交点分别为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设点![]() (
(![]() 且
且![]() )为椭圆
)为椭圆![]() 上一点,点
上一点,点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,直线
,直线![]() ,
,![]() 分别交
分别交![]() 轴于点
轴于点![]() ,
,![]() .试判断
.试判断![]() 是否为定值?若是求出该定值,若不是定值,请说明理由.
是否为定值?若是求出该定值,若不是定值,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】蔬菜批发市场销售某种蔬菜,在一个销售周期内,每售出1吨该蔬菜获利500元,未售出的蔬菜低价处理,每吨亏损100元.统计该蔬菜以往100个销售周期的市场需求量,绘制下图所示频率分布直方图.
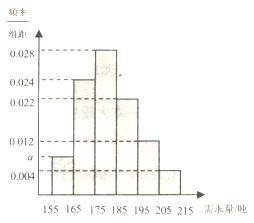
(Ⅰ)求![]() 的值,并求100个销售周期的平均市场需求量(以各组的区间中点值代表该组的数值);
的值,并求100个销售周期的平均市场需求量(以各组的区间中点值代表该组的数值);
(Ⅱ)若经销商在下个销售周期购进了190吨该蔬菜,设![]() 为该销售周期的利润(单位:元),
为该销售周期的利润(单位:元),![]() 为该销售周期的市场需求量(单位:吨).求
为该销售周期的市场需求量(单位:吨).求![]() 与
与![]() 的函数解析式,并估计销售的利润不少于86000元的概率.
的函数解析式,并估计销售的利润不少于86000元的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】A地的天气预报显示,A地在今后的三天中,每一天有强浓雾的概率为![]() ,现用随机模拟的方法估计这三天中至少有两天有强浓雾的概率,先利用计算器产生
,现用随机模拟的方法估计这三天中至少有两天有强浓雾的概率,先利用计算器产生![]() 之间整数值的随机数,并用0,1,2,3,4,5,6表示没有强浓雾,用7,8,9表示有强浓雾,再以每3个随机数作为一组,代表三天的天气情况,产生了如下20组随机数:
之间整数值的随机数,并用0,1,2,3,4,5,6表示没有强浓雾,用7,8,9表示有强浓雾,再以每3个随机数作为一组,代表三天的天气情况,产生了如下20组随机数:
402 978 191 925 273 842 812 479 569 683
231 357 394 027 506 588 730 113 537 779
则这三天中至少有两天有强浓雾的概率近似为![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线C:![]() (
(![]() )的焦点F到准线l的距离为2,直线
)的焦点F到准线l的距离为2,直线![]() 过点F且与抛物线交于M、N两点,直线
过点F且与抛物线交于M、N两点,直线![]() 过坐标原点O及点M且与l交于点P,点Q在线段
过坐标原点O及点M且与l交于点P,点Q在线段![]() 上.
上.
(1)求直线![]() 的斜率;
的斜率;
(2)若![]() ,
,![]() ,
,![]() 成等差数列,求点Q的轨迹方程.
成等差数列,求点Q的轨迹方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com