【题目】（题文）已知函数，其中为正实数.

（1）若函数在处的切线斜率为2，求的值；

（2）求函数的单调区间；

（3）若函数有两个极值点，求证：

【题目】某地环保部门跟踪调查一种有害昆虫的数量．根据调查数据，该昆虫的数量（万只）与时间（年）（其中）的关系为．为有效控制有害昆虫数量、保护生态环境，环保部门通过实时监控比值（其中为常数，且）来进行生态环境分析．

（1）当时，求比值取最小值时的值；

（2）经过调查，环保部门发现：当比值不超过时不需要进行环境防护．为确保恰好3年不需要进行保护，求实数的取值范围．（为自然对数的底， ）

【题目】在边长为8正方形中，点为的中点，是上一点，且，若对于常数，在正方形的边上恰有个不同的点，使得，则实数的取值范围为______.

（1）当a＝1时，解不等式f（x）＞x+1；

（2）若存在实数x，使得f（x）f（x+1），求实数a的取值范围．

【题目】在平面直角坐标系xOy中，曲线C的参数方程为，（θ为参数），以原点为极点，x轴非负半轴为极轴建立极坐标系．

（1）求曲线C的极坐标方程；

（2）在平面直角坐标系xOy中，A（﹣2，0），B（0，﹣2），M是曲线C上任意一点，求△ABM面积的最小值．

【题目】已知函数．

(1)若，求函数的所有零点；

(2)若，证明函数不存在极值．

【题目】新能源汽车是战略性新兴行业之一，发展新能源汽车是中国从汽车大国迈向汽车强国的必由之路，某汽车企业为了适应市场需求引进了新能源汽车生产设备，2019年该企业新能源汽车的销售量逐月平稳增长，1，2，3月份的销售量分别为1.2千台，1.4千台，1.8千台，为估计以后每个月的销售量，以这三个月的销售量为依据，用一个函数模拟汽车的月销售量（单位：千台）和月份之间的函数关系，有以下两个函数模型可供选择：

①；②，如果4月份的销售量为2.3千台，选择一个效果较好的函数进行模拟，则估计5月份的销售量为________千台.

【题目】如图，矩形所在的平面垂直于平面，为的中点，，，，.

（1）求异面直线与所成角的余弦值；

（2）求二面角的正弦值.

【题目】设函数，，.

（1）求函数的单调区间；

（2）若函数有两个零点，().

（i）求的取值范围；

（ii）求证:随着的增大而增大.

【题目】一酒企为扩大生产规模，决定新建一个底面为长方形的室内发酵馆，发酵馆内有一个无盖长方体发酵池，其底面为长方形(如图所示)，其中.结合现有的生产规模，设定修建的发酵池容积为450米，深2米.若池底和池壁每平方米的造价分别为200元和150元，发酵池造价总费用不超过65400元

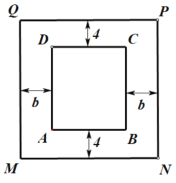
（1）求发酵池边长的范围；

（2）在建发酵馆时，发酵池的四周要分别留出两条宽为4米和米的走道（为常数）.问:发酵池的边长如何设计，可使得发酵馆占地面积最小.