【题目】（题文）（题文）已知椭圆的离心率为,过右焦点且斜率为1的直线交椭圆于A,B两点, N为弦AB的中点,O为坐标原点.

(1)求直线ON的斜率；

(2)求证:对于椭圆上的任意一点M,都存在,使得成立.

【题目】已知曲线C的极坐标方程是.以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线l的参数方程是: 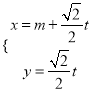(是参数).

(Ⅰ)将曲线C的极坐标方程化为直角坐标方程,将直线的参数方程化为普通方程;

(Ⅱ)若直线l与曲线C相交于A、B两点,且,试求实数m的值.

【题目】已知函数．

（1）求函数的极值；

（2）对于曲线上的不同两点，如果存在曲线上的点，且使得曲线在点处的切线，则称为弦的伴随直线，特别地，当时，又称为的—伴随直线．

①求证：曲线的任意一条弦均有伴随直线，并且伴随直线是唯一的；

②是否存在曲线，使得曲线的任意一条弦均有—伴随直线？若存在，给出一条这样的曲线，并证明你的结论；若不存在，说明理由．

【题目】直线ax＋by＝1与圆x2＋y2＝1相交于A，B两点(其中a，b是实数)，且△AOB是直角三角形(O是坐标原点)，则点P(a，b)与点(0,1)之间距离的最小值为( )．

A.0B.C.－1D.＋1

【题目】如图a是某市参加2012年高考的学生身高条形统计图，从左到右的各条形表示的学生人数依次记为、、…、[如表示身高（单位：cm）在内的学生人数]．图b是统计图a中身高在一定范围内学生人数的一个算法流程图．现要统计身高在（含160cm，不含180cm）的学生人数，那么在流程图中的判断框内应填写的条件是（ ）

A.B.C.D.

【题目】《数书九章》是中国南宋时期杰出数学家秦九韶的著作，全书十八卷共八十一个问题，分为九类，每类九个问题，《数书九章》中记录了秦九昭的许多创造性成就，其中在卷五“三斜求积”中提出了已知三角形三边，，求面积的公式，这与古希腊的海伦公式完成等价，其求法是:“以小斜幂并大斜幂减中斜幂，余半之，自乘于上，以小斜幂乘大斜幂减上，余四约之，为实，一为从隅，开平方得积.”若把以上这段文字写成公式，即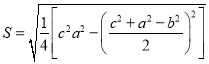.现有满足，且的面积，请运用上述公式判断下列命题正确的是

A.周长为

B.三个内角，，成等差数列

C.外接圆直径为

D.中线的长为

【题目】设函数，.

（1）若，求函数的单调区间；

（2）若，且函数在区间内有两个极值点，求实数a的取值范围；

（3）求证：对任意的正数a，都存在实数t，满足：对任意的，.

【题目】已知数列满足：（常数），（，）.数列满足：（）.

（1）求，的值；

（2）求数列的通项公式；

（3）是否存在k，使得数列的每一项均为整数？若存在，求出k的所有可能值；若不存在，请说明理由.

【题目】如图，，是某景区的两条道路（宽度忽略不计，为东西方向），Q为景区内一景点，A为道路上一游客休息区，已知，（百米），Q到直线，的距离分别为3（百米），（百米），现新修一条自A经过Q的有轨观光直路并延伸至道路于点B，并在B处修建一游客休息区.

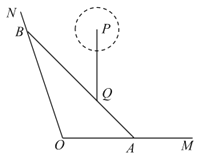
（1）求有轨观光直路的长；

（2）已知在景点Q的正北方6百米的P处有一大型组合音乐喷泉，喷泉表演一次的时长为9分钟，表演时，喷泉喷洒区域以P为圆心，r为半径变化，且t分钟时，（百米）（，）.当喷泉表演开始时，一观光车S（大小忽略不计）正从休息区B沿（1）中的轨道以（百米/分钟）的速度开往休息区A，问：观光车在行驶途中是否会被喷泉喷洒到，并说明理由.

【题目】在平面直角坐标系中，已知椭圆E：（）过点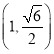，其心率等于.

（1）求椭圆E的标准方程；

（2）若A，B分别是椭圆E的左，右顶点，动点M满足，且椭圆E于点P.

①求证：为定值：

②设与以为直径的圆的另一交点为Q，求证：直线经过定点.