
科目: 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为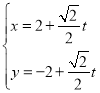 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程是
的极坐标方程是![]() .
.
(1)求曲线![]() 的直角坐标方程和直线
的直角坐标方程和直线![]() 的普通方程;
的普通方程;
(2)设点![]() ,
,![]() 为曲线
为曲线![]() 上的动点,求
上的动点,求![]() 的面积的最大值.
的面积的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() 为非零实数.
为非零实数.
(1)求![]() 的极值;
的极值;
(2)当![]() 时,在函数
时,在函数![]() 的图象上任取两个不同的点
的图象上任取两个不同的点![]() 、
、![]() .若当
.若当![]() 时,总有不等式
时,总有不等式![]() 成立,求正实数
成立,求正实数![]() 的取值范围:
的取值范围:
(3)当![]() 时,设
时,设![]() 、
、![]() ,证明:
,证明:![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】某人沿固定路线开车上班,沿途共有![]() 个红绿灯,他对过去
个红绿灯,他对过去![]() 个工作日上班途中的路况进行了统计,得到了如表的数据:
个工作日上班途中的路况进行了统计,得到了如表的数据:
上班路上遇见的红灯数 |
|
|
|
|
|
|
天数 |
|
|
|
|
|
|
若一路绿灯,则他从家到达公司只需用时![]() 分钟,每遇一个红灯,则会多耗时
分钟,每遇一个红灯,则会多耗时![]() 分钟,以频率作为概率的估计值
分钟,以频率作为概率的估计值
(1)试估计他平均每天上班需要用时多少分钟?
(2)若想以不少于![]() 的概率在早上
的概率在早上![]() 点前(含
点前(含![]() 点)到达公司,他最晚何时要离家去公司?
点)到达公司,他最晚何时要离家去公司?
(3)公司规定,员工应早上![]() 点(含
点(含![]() 点)前打卡考勤,否则视为迟到,每迟到一次,会被罚款
点)前打卡考勤,否则视为迟到,每迟到一次,会被罚款![]() 元.因某些客观原因,在接下来的
元.因某些客观原因,在接下来的![]() 个工作日里,他每天早上只能
个工作日里,他每天早上只能![]() 从家出发去公司,求他因迟到而被罚款的期望.
从家出发去公司,求他因迟到而被罚款的期望.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,点
,点![]() 是抛物线
是抛物线![]() 上一点,且满足
上一点,且满足![]() .
.
(1)求![]() 、
、![]() 的值;
的值;
(2)设![]() 、
、![]() 是抛物线
是抛物线![]() 上不与
上不与![]() 重合的两个动点,记直线
重合的两个动点,记直线![]() 、
、![]() 与
与![]() 的准线的交点分别为
的准线的交点分别为![]() 、
、![]() ,若
,若![]() ,问直线
,问直线![]() 是否过定点?若是,则求出该定点坐标,否则请说明理由.
是否过定点?若是,则求出该定点坐标,否则请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】下列说法错误的是( )
A.“![]() ”是“
”是“![]() ”的充分不必要条件
”的充分不必要条件
B.若![]() 为假命题,则
为假命题,则![]() ,
,![]() 均为真命题
均为真命题
C.命题“若![]() ,则
,则![]() ”的逆否命题是“若
”的逆否命题是“若![]() ,则
,则![]() |”
|”
D.若命题![]() ,使得
,使得![]() ,则
,则![]() ,恒有
,恒有![]()
查看答案和解析>>
科目: 来源: 题型:
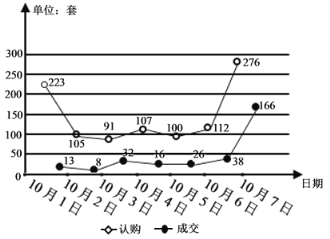
【题目】某地在国庆节![]() 天假期中的楼房认购量(单位:套)与成交量(单位:套)的折线图如图所示,小明同学根据折线图对这
天假期中的楼房认购量(单位:套)与成交量(单位:套)的折线图如图所示,小明同学根据折线图对这![]() 天的认购量与成交量作出如下判断:①成交量的中位数为
天的认购量与成交量作出如下判断:①成交量的中位数为![]() ;②认购量与日期正相关;③日成交量超过日平均成交量的有
;②认购量与日期正相关;③日成交量超过日平均成交量的有![]() 天,则上述判断中正确的个数为( )
天,则上述判断中正确的个数为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系xOy中,以坐标原点O为极点,以x轴正半轴为极轴,建立极坐标系,曲线C的极坐标方程为![]() 射线
射线![]() 交曲线C于点A,倾斜角为α的直线l过线段OA的中点B且与曲线C交于P、Q两点.
交曲线C于点A,倾斜角为α的直线l过线段OA的中点B且与曲线C交于P、Q两点.
(1)求曲线C的直角坐标方程及直线l的参数方程;
(2)当直线l倾斜角α为何值时, |BP|·|BQ|取最小值, 并求出|BP|·|BQ|最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知平面上动点![]() 到点
到点![]() 距离比它到直线
距离比它到直线![]() 距离少1.
距离少1.
(1)求动点![]() 的轨迹方程;
的轨迹方程;
(2)记动点![]() 的轨迹为曲线
的轨迹为曲线![]() ,过点
,过点![]() 作直线
作直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,点
两点,点![]() ,延长
,延长![]() ,
,![]() ,与曲线
,与曲线![]() 交于
交于![]() ,
,![]() 两点,若直线
两点,若直线![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,试探究
,试探究![]() 是否为定值?若为定值,请求出定值,若不为定值,请说明理由.
是否为定值?若为定值,请求出定值,若不为定值,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】从某工厂生产的某种产品中抽取1000件,测量这些产品的一项质量指标值,由测量结果得如下频率分布直方图:
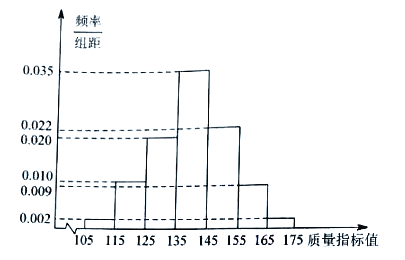
(1)求这1000件产品质量指标值的样本平均数![]() 和样本方差
和样本方差![]() (同一组数据用该区间的中点值作代表)
(同一组数据用该区间的中点值作代表)
(2)由频率分布直方图可以认为,这种产品的质量指标值![]() 服从正态分布
服从正态分布![]() ,其中以
,其中以![]() 近似为样本平均数
近似为样本平均数![]() ,
,![]() 近似为样本方差
近似为样本方差![]() .
.
(ⅰ)利用该正态分布,求![]() ;
;
(ⅱ)某用户从该工厂购买了100件这种产品,记![]() 表示这100件产品中质量指标值为于区间(127.6,140)的产品件数,利用(ⅰ)的结果,求
表示这100件产品中质量指标值为于区间(127.6,140)的产品件数,利用(ⅰ)的结果,求![]() .
.
附:![]() .若
.若![]() ,则
,则![]() ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com