
科目: 来源: 题型:
【题目】已知抛物线![]() 与直线l:y=kx﹣1无交点,设点P为直线l上的动点,过P作抛物线C的两条切线,A,B为切点.
与直线l:y=kx﹣1无交点,设点P为直线l上的动点,过P作抛物线C的两条切线,A,B为切点.
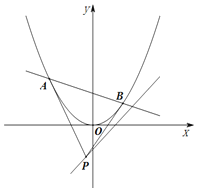
(1)证明:直线AB恒过定点Q;
(2)试求△PAB面积的最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,∠BAC=90°,AB=AC=AA1.

(1)求证:AB1⊥平面A1BC1;
(2)若D在B1C1上,满足B1D=2DC1,求AD与平面A1BC1所成的角的正弦值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知三棱锥P﹣ABC的所有棱长为1.M是底面△ABC内部一个动点(包括边界),且M到三个侧面PAB,PBC,PAC的距离h1,h2,h3成单调递增的等差数列,记PM与AB,BC,AC所成的角分别为α,β,γ,则下列正确的是( )
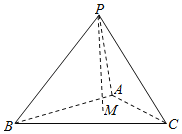
A.α=βB.β=γC.α<βD.β<γ
查看答案和解析>>
科目: 来源: 题型:
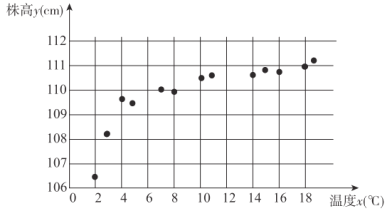
【题目】一种室内种植的珍贵草药的株高![]() (单位:
(单位:![]() )与一定范围内的温度
)与一定范围内的温度![]() (单位:
(单位:![]() )有关,现收集了该种草药的13组观测数据,得到如下的散点图,现根据散点图利用
)有关,现收集了该种草药的13组观测数据,得到如下的散点图,现根据散点图利用![]() 或
或![]() 建立
建立![]() 关于
关于![]() 的回归方程,令
的回归方程,令![]() ,
,![]() ,得到如下数据,且
,得到如下数据,且![]() 与
与![]() (
(![]() )的相关系数分别为
)的相关系数分别为![]() ,且
,且![]() .
.
|
|
|
|
10.15 | 109.94 | 3.04 | 0.16 |
|
|
|
|
|
|
|
|
|
|
(1)用相关系数说明哪种模型建立![]() 与
与![]() 的回归方程更合适;
的回归方程更合适;
(2)根据(1)的结果及表中数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
(3)已知这种草药的利润![]() 与
与![]() ,
,![]() 的关系为
的关系为![]() ,当
,当![]() 为何值时,利润
为何值时,利润![]() 的预报值最大.
的预报值最大.
附:参考公式和数据:对于一组数据![]() (
(![]() ),其回归直线
),其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为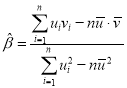 ,
,![]() ,相关系数
,相关系数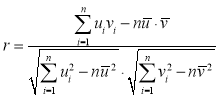 ,
,![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】2020年2月1日0:00时,英国顺利“脱欧”.在此之前,英国“脱欧”这件国际大事被社会各界广泛关注,英国大选之后,曾预计将会在2020年1月31日完成“脱欧”,但是因为之前“脱欧”一直被延时,所以很多人认为并不能如期完成,某媒体随机在人群中抽取了100人做调查,其中40岁以上的55人中有10人认为不能完成,40岁以下的人中认为能完成的占![]() .
.
(1)完成![]() 列联表,并回答能否有90%的把握认为“预测国际大事的准确率与年龄有关”?
列联表,并回答能否有90%的把握认为“预测国际大事的准确率与年龄有关”?
能完成 | 不能完成 | 合计 | |
40岁以上 | |||
40岁以下 | |||
合计 |
(2)从上述100人中,采用按年龄分层抽样的方法,抽取20人,从这20人中再选取40岁以下的2人做深度调査,则2人中恰有1人认为英国能够完成“脱欧”的概率为多少?
附表:
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
参考公式为:
查看答案和解析>>
科目: 来源: 题型:
【题目】大约在20世纪30年代,世界上许多国家都流传着这样一个题目:任取一个正整数![]() ,如果它是偶数,则除以2;如果它是奇数,则将它乘以3加1,这样反复运算,最后结果必然是1.这个题目在东方被称为“角谷猜想”,世界一流的大数学家都被其卷入其中,用尽了各种方法,甚至动用了最先进的电子计算机,验算到对700亿以内的自然数上述结论均为正确的,但却给不出一般性的证明.例如取
,如果它是偶数,则除以2;如果它是奇数,则将它乘以3加1,这样反复运算,最后结果必然是1.这个题目在东方被称为“角谷猜想”,世界一流的大数学家都被其卷入其中,用尽了各种方法,甚至动用了最先进的电子计算机,验算到对700亿以内的自然数上述结论均为正确的,但却给不出一般性的证明.例如取![]() ,则要想算出结果1,共需要经过的运算步数是( )
,则要想算出结果1,共需要经过的运算步数是( )
A.9B.10C.11D.12
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() 的离心率
的离心率![]() ,
,![]() ,
,![]() ,
,![]() 是椭圆上三个不同的点,F为其右焦点,且
是椭圆上三个不同的点,F为其右焦点,且![]() ,
,![]() ,
,![]() 成等差数列
成等差数列
(1)求椭圆的方程;
(2)求![]() 的值;
的值;
(3)若线段AC的垂直平分线与x轴交点为D,求直线BD的斜率k.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com