
科目: 来源: 题型:
【题目】随着经济全球化信息化的发展,企业之间的竞争从资源的争夺转向人才的竞争.吸引留住培养和用好人才成为人力资源管理的战略目标和紧迫任务.在此背景下,某信息网站在15个城市中对刚毕业的大学生的月平均收入薪资和月平均期望薪资做了调查,数据如下图所示.
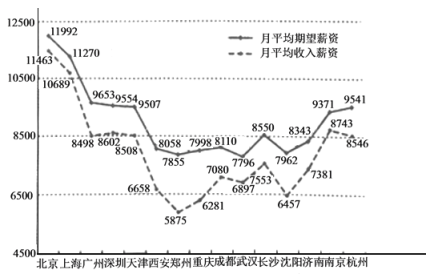
(1)若某大学毕业生从这15座城市中随机选择一座城市就业,求该生选中月平均收入薪资高于8500元的城市的概率;
(2)若从月平均收入薪资与月平均期望薪资之差高于1000元的城市中随机选择2座城市,求这2座城市的月平均期望薪资都低于8500元的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系![]() 中,以
中,以![]() 为极点,
为极点,![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ;直线
;直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),直线
为参数),直线![]() 与曲线
与曲线![]() 分别交于
分别交于![]() ,
,![]() 两点.
两点.
(1)写出曲线![]() 的直角坐标方程和直线
的直角坐标方程和直线![]() 的普通方程;
的普通方程;
(2)若点![]() 的极坐标为
的极坐标为![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】在四棱锥![]() 中,底面
中,底面![]() 为平行四边形,
为平行四边形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 点在底面
点在底面![]() 内的射影
内的射影![]() 在线段
在线段![]() 上,且
上,且![]() ,
, ![]() ,M在线段
,M在线段![]() 上,且
上,且![]() .
.
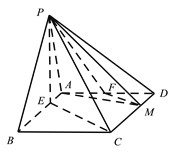
(Ⅰ)证明: ![]() 平面
平面![]() ;
;
(Ⅱ)在线段AD上确定一点F,使得平面![]() 平面PAB,并求三棱锥
平面PAB,并求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知![]() ,
,![]() 为椭圆
为椭圆![]() 的左右焦点,
的左右焦点,![]() 在以
在以![]() 为圆心,1为半径的圆
为圆心,1为半径的圆![]() 上,且
上,且![]() .
.
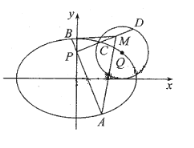
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
,![]() 两点,过
两点,过![]() 与
与![]() 垂直的直线
垂直的直线![]() 交圆
交圆![]() 于
于![]() ,
,![]() 两点,
两点,![]() 为线段
为线段![]() 的中点,求
的中点,求![]() 的面积的取值范围.
的面积的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】在《九章算术》中,将四个面都为直角三角形的四面体称之为鳖臑.如图,在鳖臑![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,且
,且![]() ,过点
,过点![]() 分别作
分别作![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,连结
,连结![]() ,当
,当![]() 的面积最大值时,
的面积最大值时,![]() ( ).
( ).
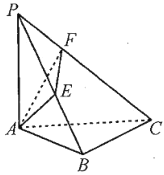
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() ,
,![]() .
.
(1)若数列![]() 是等差数列,且
是等差数列,且![]() ,求实数
,求实数![]() 的值;
的值;
(2)若数列![]() 满足
满足![]()
![]() ,且
,且![]() ,求证:数列
,求证:数列![]() 是等差数列;
是等差数列;
(3)设数列![]() 是等比数列,试探究当正实数
是等比数列,试探究当正实数![]() 满足什么条件时,数列
满足什么条件时,数列![]() 具有如下性质
具有如下性质![]() :对于任意的
:对于任意的![]()
![]() ,都存在
,都存在![]() 使得
使得![]() ,写出你的探求过程,并求出满足条件的正实数
,写出你的探求过程,并求出满足条件的正实数![]() 的集合.
的集合.
查看答案和解析>>
科目: 来源: 题型:
【题目】数列![]() 的前n项和为
的前n项和为![]() ,若数列
,若数列![]() 的各项按如下规律排列:
的各项按如下规律排列:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,…,
,…,![]() ,…有如下运算和结论:①
,…有如下运算和结论:①![]() ;②数列
;②数列![]() ,
,![]() ,
,![]() ,
,![]() ,…是等比数列;③数列
,…是等比数列;③数列![]() ,
,![]() ,
,![]() ,
,![]() ,…的前
,…的前![]() 项和为
项和为![]() ;④若存在正整数
;④若存在正整数![]() ,使
,使![]() ,
,![]() ,则
,则![]() .其中正确的结论是_____.(将你认为正确的结论序号都填上)
.其中正确的结论是_____.(将你认为正确的结论序号都填上)
查看答案和解析>>
科目: 来源: 题型:
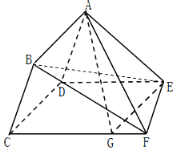
【题目】如图,在多面体ABCDEF中,四边形ABCD为平行四边形,平面ADE⊥平面CDEF,∠ADE=60°,DE∥CF,CD⊥DE,AD=2,DE=DC=3,CF=4,点G是棱CF上的动点.
(Ⅰ)当CG=3时,求证EG∥平面ABF;
(Ⅱ)求直线BE与平面ABCD所成角的正弦值;
(Ⅲ)若二面角G﹣AE﹣D所成角的余弦值为![]() ,求线段CG的长.
,求线段CG的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com