
科目: 来源: 题型:
【题目】在讨论勾股定理的过程中,《九章算术》提供了许多整勾股数,如![]() ,等等.其中最大的数称为“弦数”,后人在此基础上进一步研究,得到如下规律:若勾股数组中的某一个数
,等等.其中最大的数称为“弦数”,后人在此基础上进一步研究,得到如下规律:若勾股数组中的某一个数![]() 是确定的奇数(大于1),把它平方后拆成相邻的两个整数,那么奇数与这两个整数构成一组勾股数,若勾股数组中的某一个数
是确定的奇数(大于1),把它平方后拆成相邻的两个整数,那么奇数与这两个整数构成一组勾股数,若勾股数组中的某一个数![]() 是大于2的偶数,把它除以2后再平方,然后把这个平方数分别减1,加1所得到的两个整数和这个偶数构成一组勾股数.由此得到的这种勾股数称之为“由
是大于2的偶数,把它除以2后再平方,然后把这个平方数分别减1,加1所得到的两个整数和这个偶数构成一组勾股数.由此得到的这种勾股数称之为“由![]() 生成的一组勾股数”.若“由17生成的这组勾股数”的“弦数”为
生成的一组勾股数”.若“由17生成的这组勾股数”的“弦数”为![]() ,“由20生成的这组勾股数”的“弦数”为
,“由20生成的这组勾股数”的“弦数”为![]() ,则
,则![]() ____________.
____________.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知直线![]() 的参数方程为
的参数方程为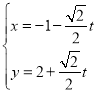 (其中
(其中![]() 为参数),以原点为极点,以
为参数),以原点为极点,以![]() 轴为极轴建立极坐标系,曲线
轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() (
(![]() 为常数,且
为常数,且![]() ),直线
),直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点.
两点.
(1)若![]() ,求实数
,求实数![]() 的值;
的值;
(2)若点![]() 的直角坐标为
的直角坐标为![]() ,且
,且![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】随着新政策的实施,海淘免税时代于2016年4月8日正式结束,新政策实施后,海外购物的费用可能会增加.为了解新制度对海淘的影响,某网站调查了喜欢海淘的1000名网友,其态度共有两类:第一类是会降低海淘数量,共有400人,第二类是不会降低海淘数量,共有600人,若从这1000人中按照分层抽样的方法抽取10人后进行打分,其打分的茎叶图如下图所示,图中有数据缺失,但已知“第一类”和“第二类”网民打分的均值相等,则“第一类”网民打分的方差为( )
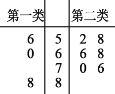
A.159B.179C.189D.209
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]()
![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,离心率为
,离心率为![]() ,且
,且![]() 在椭圆
在椭圆![]() 上运动,当点
上运动,当点![]() 恰好在直线l:
恰好在直线l:![]() 上时,
上时,![]() 的面积为
的面积为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)作与![]() 平行的直线
平行的直线![]() ,与椭圆交于
,与椭圆交于![]() 两点,且线段
两点,且线段![]() 的中点为
的中点为![]() ,若
,若![]() 的斜率分别为
的斜率分别为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】2016年5月20日以来,广东自西北到东南出现了一次明显降雨.为了对某地的降雨情况进行统计,气象部门对当地20日~28日9天内记录了其中100小时的降雨情况,得到每小时降雨情况的频率分布直方图如下:
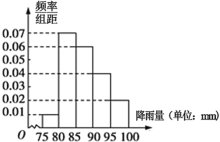
若根据往年防汛经验,每小时降雨量在![]() 时,要保持二级警戒,每小时降雨量在
时,要保持二级警戒,每小时降雨量在![]() 时,要保持一级警戒.
时,要保持一级警戒.
(1)若以每组的中点代表该组数据值,求这100小时内每小时的平均降雨量;
(2)若从记录的这100小时中按照警戒级别采用分层抽样的方法抽取10小时进行深度分析.再从这10小时中随机抽取3小时,求抽取的这3小时中属于一级警戒时间的分布列与数学期望.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知直线![]() 的参数方程为
的参数方程为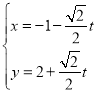 (其中
(其中![]() 为参数),以原点为极点,以
为参数),以原点为极点,以![]() 轴为极轴建立极坐标系,曲线
轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() (
(![]() 为常数,且
为常数,且![]() ),直线
),直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点.
两点.
(1)若![]() ,求实数
,求实数![]() 的值;
的值;
(2)若点![]() 的直角坐标为
的直角坐标为![]() ,且
,且![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】随着新政策的实施,海淘免税时代于2016年4月8日正式结束,新政策实施后,海外购物的费用可能会增加.为了解新制度对海淘的影响,某记者调查了身边喜欢海淘的10位朋友,其态度共有两类:第一类是会降低海淘数量,共有4人,第二类是不会降低海淘数量,共有6人.若该记者计划从这10人中随机选取5人按顺序进行采访,则“第一类”的人数多于“第二类”,且采访中“第二类”不连续进行的不同采访顺序有( )
A.3840B.5040C.6020D.7200
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() 的左顶点为
的左顶点为![]() ,右焦点为
,右焦点为![]() ,
,![]() 为椭圆
为椭圆![]() 上两点,圆
上两点,圆![]() .
.
(1)若![]() 轴,且满足直线
轴,且满足直线![]() 与圆
与圆![]() 相切,求圆
相切,求圆![]() 的方程;
的方程;
(2)若圆![]() 的半径为
的半径为![]() ,点
,点![]() 满足
满足![]() ,求直线
,求直线![]() 被圆
被圆![]() 截得弦长的最大值.
截得弦长的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com