A.256B.350C.162D.96

【题目】在直角坐标系xOy中，以O为极点，x轴的正半轴为极轴建立极坐标系，直线l的极坐标方程为，Q为l上的动点，以OQ为边作等边三角形OPQ，且三点O，P，Q按逆时针方向排列.

（Ⅰ）设点P运动轨迹E的直角坐标方程；

（Ⅱ）若曲线经过伸缩变换得到曲线，若点M为曲线上的动点，且点M到曲线E的最小距离为1，求实数a的值.

【题目】已知函数.

（Ⅰ）若函数，求函数的单调区间；

（Ⅱ）设直线l为函数的图象上一点处的切线，证明：在区间上存在唯一的，使得直线l与曲线相切并求出此时n的值.（参考数据：）

【题目】已知在三棱柱中，，，，平面平面ABC，M为的中点，D为AB中点.

（Ⅰ）证明：平面ACM.

（Ⅱ）求三棱柱的侧面积.

统计结果显示100位顾客中购物款不低于100元的顾客占60%，据统计该商场每日大约有5000名顾客，为了增加商场销售额度，对一次性购物不低于100元的顾客发放纪念品（每人一件）．（注：视频率为概率）

（1）试确定的值，并估计该商场每日应准备纪念品的数量；

（2）为了迎接店庆，商场进行让利活动，一次购物款200元及以上的一次返利30元；一次性购物

款小于200元的按购物款的百分比返利，具体见下表：

估计该商场日均让利多少元？

如图，已知抛物线，过点任作一直线与相交于两点，过点作轴的平行线与直线相交于点（为坐标原点）.

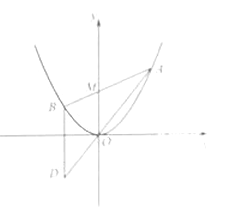
(1)证明：动点在定直线上；

(2)作的任意一条切线（不含轴）与直线相交于点，与（1）中的定直线相交于点，证明：为定值，并求此定值.

【题目】将函数的图象向右平移个单位，在向上平移一个单位，得到g（x）的图象．若g（x1）g（x2）＝4，且x1，x2∈[﹣2π，2π]，则x1﹣2x2的最大值为（　　）

A. B. C. D.

【题目】已知函数，．

（1）若在点处的切线与直线垂直，求函数在点处的切线方程；

（2）若对于，恒成立，求正实数的取值范围；

（3）设函数，且函数有极大值点，求证：.

【题目】设是等比数列的公比大于，其前项和为，是等差数列，已知，，，.

（1）求，的通项公式

（2）设，数列的前项和为，求；

（3）设，其中,求

【题目】已知椭圆的左、右焦点分别为、，且，椭圆经过点.

（1）求椭圆的方程；

（2）直线过椭圆右顶点，交椭圆于另一点，点在直线上，且.若，求直线的斜率．